
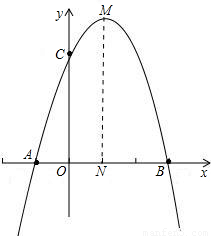
 解:(1)由题意,可设抛物线的解析式为y=a(x+1)(x-3).
解:(1)由题意,可设抛物线的解析式为y=a(x+1)(x-3). •OA•OC+
•OA•OC+ •BN•MN+
•BN•MN+ (OC+MN)•ON
(OC+MN)•ON ×1×3+
×1×3+ ×2×4+
×2×4+ ×(3+4)×1
×(3+4)×1

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源:2011年广东省深圳市岭秀教育第一次诊断性测数学试卷(解析版) 题型:解答题
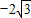 ),抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
),抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
查看答案和解析>>
科目:初中数学 来源:2011年浙江省杭州市中考数学模拟试卷(15)(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2009年云南省楚雄州双柏县中考数学模拟试卷(民族中学)(解析版) 题型:选择题
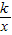 (k≠0)的图象大致为( )
(k≠0)的图象大致为( )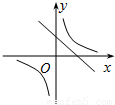
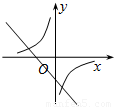
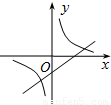
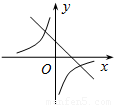
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com