
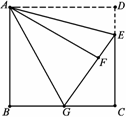
如图,有一正方形的纸片ABCD,边长为3,点E是DC边上一点且DE=![]() DC,把△ADE沿AE折叠使△ADE落在△AFE的位置,延长EF交BC边于点G,连接AG.有以下四个结论 ①∠GAE=45° ②BG+DE=GE ③点G是BC的中点 ④
DC,把△ADE沿AE折叠使△ADE落在△AFE的位置,延长EF交BC边于点G,连接AG.有以下四个结论 ①∠GAE=45° ②BG+DE=GE ③点G是BC的中点 ④![]()
(1)其中正确的结论序号是 .
(2)请选一个你认为正确的结论进行说理论证.
(1)①②③④ ……………………………………………………………………………3分
(2)∵△AFE是△ADE折叠而得到的
∴△![]() ADE≌△AFE∴∠DAE=∠FAE,AD=AF
ADE≌△AFE∴∠DAE=∠FAE,AD=AF
∵四边形ABCD是正方形
∴AD=AB,∠A=∠B=90°
∵∠AFE=∠ADE=90º∴∠AFG=90º
∵AG=AG,AB=AF∴Rt△ABG≌Rt△AFG(HL)………………………………………6分
∴∠BAG=∠FAG
∵∠BAG+∠GAF+∠FAE+∠EAD=90°
∴∠GAF+∠FAE=45º
即∠GAE=45º………………………………………………………………………………9分
【相关知识点】全等三角形的性质和判定,勾股定理及一元二次方程
【解题思路】由折叠易得∠DAE=∠FAE,再证∠BAG=∠FAG可得∠GAE=45º,若证②③④也可.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
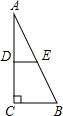 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一
如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一![]() 个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为
个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为
( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(浙江杭州卷)数学 题型:选择题
(2011•滨州)如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )

A、1 B、2
C、3 D、4
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(山东滨州卷)数学 题型:选择题
(2011•滨州)如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )

A、1 B、2
C、3 D、4
查看答案和解析>>
科目:初中数学 来源:《第3章 证明(三)》2011年单元测试卷(九江县城门中学)(解析版) 题型:选择题
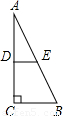
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com