
【题目】如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:
①点E和点F,点B和点D是关于中心O对称点;
②直线BD必经过点O;
③四边形DEOC与四边形BFOA的面积必相等;
④△AOE与△COF成中心对称.
其中正确的个数为( )

A.1 B.2 C.3 D.4
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】疫情期间,某地向武汉捐赠口罩1200000只,其中数1200000用科学记数法表示是( )
A.12×105B.12×106C.1.2×105D.1.2×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
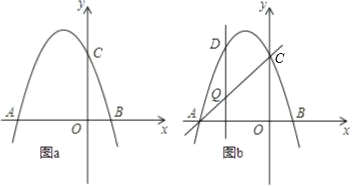
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】H7N9时一种新型禽流感,其病毒颗粒呈多形性,其中球形病毒的最大直径为0.00000012米,这一直径用科学记数法表示为( )
A.1.2×10﹣7米
B.1.2×10﹣8米
C.12×10﹣8米
D.12×10﹣9米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图①,将两块全等的三角板拼在一起,其中△ABC的边BC在直线l上,AC⊥BC且AC = BC;△EFP的边FP也在直线l上,边EF与边AC重合,EF⊥FP且EF = FP。
(1)在图①中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将三角板△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
(3)将三角板△EFP沿直线l向左平移到图③的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ。你认为(2)中猜想的BQ与AP所满足的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com