
分析 根据新定义得到x+(x+1)2=5,整理得x2+3x-4=0,再利用因式分解法解方程得到x1=-4(舍去),x2=1,然后根据新定义的条件确定x的值.
解答 解:∵x*(x+1)=5,
∴x+(x+1)2=5,
整理得x2+3x-4=0,
(x+4)(x-1)=0,
所以x1=-4(舍去),x2=1,
即x=1
故答案为x=1.
点评 本题考查了解一元二次方程-因式分解法:就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
 如图,锐角△ABC是⊙O内接三角形,弦AE⊥BC,垂足为D.在AD上取点F,使FD=DE,连接CF,并延长交AB于点G.求证:CG⊥AB.
如图,锐角△ABC是⊙O内接三角形,弦AE⊥BC,垂足为D.在AD上取点F,使FD=DE,连接CF,并延长交AB于点G.求证:CG⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
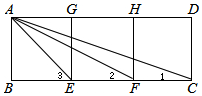 如图,四边形ABEG、GEFH、HFCD都是边长相等的正方形
如图,四边形ABEG、GEFH、HFCD都是边长相等的正方形查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种 食物 | 乙种 食物 | 丙种 食物 | 每千克生产成本(元) | |||
| 甲种食物 | 9 | |||||
| 维生素A(单位/千克) | 400 | 600 | 400 | 乙种食物 | 12 | |
| 维生素B(单位/千克) | 800 | 200 | 400 | 丙种食物 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com