数形结合的基本思想，就是在研究问题的过程中，注意把数和形结合起来考察，斟酌问题的具体情形，把图形性质的问题转化为数量关系的问题，或者把数量关系的问题转化为图形性质的问题，使复杂问题简单化，抽象问题具体化，化难为易，获得简便易行的成功方案．
例如，求1+2+3+4+…+n的值，其中n是正整数．
对于这个求和问题，如果采用纯代数的方法（首尾两头加），问题虽然可以解决，但在求和过程中，需对n的奇偶性进行讨论．
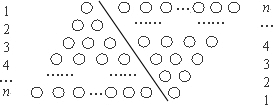
如果采用数形结合的方法，即用图形的性质来说明数量关系的事实，那就非常的直观．现利用图形的性质来求1+2+3+4+…+n的值，方案如下：如图，斜线左边的三角形图案是由上到下每层依次分别为1，2，3，…，n个小圆圈排列组成的．而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值．为求式子的值，现把左边三角形倒放于斜线右边，与原三角形组成一个平行四边形．此时，组成平行四边形的小圆圈共有n行，每行有（n+1）个小圆圈，所以组成平行四边形小圆圈的总个数为n（n+1）个，因此，组成一个三角形小圆圈的个数为
，即1+2+3+4+…+n=
．
（1）仿照上述数形结合的思想方法，设计相关图形，求1+3+5+7+…+（2n-1）的值，其中n是正整数．（要求：画出图形，并利用图形做必要的推理说明）
（2）试设计另外一种图形，求1+3+5+7+…+（2n-1）的值，其中n是正整数．（要求：画出图形，并利用图形做必要的推理说明）
，23分别填在相应的大括号内．
夺冠金卷全能练考系列答案