
 ,则此正方形的边长为________.
,则此正方形的边长为________. .以B为旋转中心,把△AEB按逆时针方向旋转60°,得△FGB,连CF,
.以B为旋转中心,把△AEB按逆时针方向旋转60°,得△FGB,连CF, +
+ ;设正方形的边长为2x,过F作FG⊥BC于G点,则FG=x,BG=
;设正方形的边长为2x,过F作FG⊥BC于G点,则FG=x,BG= x,则CG=(2+
x,则CG=(2+ )x,在Rt△FGC中,利用勾股定理即可得到x的值,则正方形的边长即可得到.
)x,在Rt△FGC中,利用勾股定理即可得到x的值,则正方形的边长即可得到.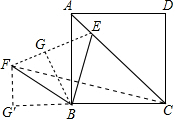 解:如图,设E到A点,B点,C点的距离之和的最小值为
解:如图,设E到A点,B点,C点的距离之和的最小值为 .
. +
+ ,
, x,则CG=(2+
x,则CG=(2+ )x,
)x, +
+ )2=x2+[(2+
)2=x2+[(2+ )x]2,
)x]2,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
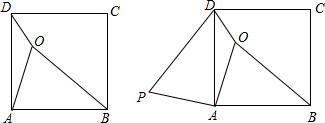
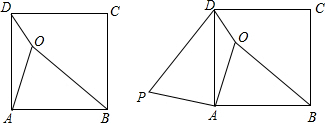 如图1,已知正方形ABCD内一点O,OD=1,OA=2,OB=3,把△OAB绕着点A逆时针旋转90°得到△PAD如图2.(1)求点O到点P的距离.(2)求∠AOD的度数.
如图1,已知正方形ABCD内一点O,OD=1,OA=2,OB=3,把△OAB绕着点A逆时针旋转90°得到△PAD如图2.(1)求点O到点P的距离.(2)求∠AOD的度数.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2008-2009学年浙江省台州市五校第二次联考九年级(上)月考数学试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com