练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    问题探究

       (1)请你在图①中做一条直线，使它将矩形ABCD分成面积相等的两部分；

     （2）如图②点M是矩形ABCD内一点，请你在图②中过点M作一条直线，使它将矩形ABCD分成面积相等的两部分。

      问题解决

    （3）    如图③，在平面直角坐标系中，直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图，其中DC∥OB,OB=6,CD=4开发区综合服务管理委员会（其占地面积不计）设在点P（4,2）处。为了方便驻区单位准备过点P修一条笔直的道路（路宽不计），并且是这条路所在的直线l将直角梯形OBCD分成面积相等的了部分，你认为直线l是否存在？若存在求出直线l的表达式；若不存在，请说明理由

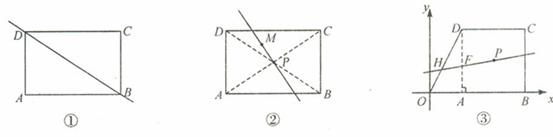
    解：（1）如图①

    （2）如图②连结AC 、BC交与P则P为矩形对称中心。作直线MP，直线MP即为所求。

    （3）    如图③存在直线l

    过点D的直线只要作 DA⊥OB与点A

    则点P(4,2)为矩形ABCD的对称中心

    ∴过点P的直线只要平分△DOA的面积即可

    易知，在OD边上必存在点H使得PH将△DOA 面积平分。

    从而，直线PH平分梯形OBCD的面积

    即直线 PH为所求直线l

    设直线PH的表达式为 y=kx+b 且点P(4,2)

    ∴2=4k+b 即b=2-4k

    ∴y=kx+2-4k

    ∵直线OD的表达式为y=2x

    解之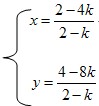

    ∴点H的坐标为（，）

    ∴PH与线段AD的交点F（2,2-2k）

    ∴0＜2-2k＜4

    ∴-1＜k＜1

    ∴S△DHF=

    ∴解之，得。（舍去）

    ∴b=8-

    ∴直线l的表达式为y=

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    25、请阅读下列材料：
    已知：如图1在Rt△ABC中，∠BAC=90°，AB=AC，点D、E分别为线段BC上两动点，若∠DAE=45度．探究线段BD、DE、EC三条线段之间的数量关系．
    小明的思路是：把△AEC绕点A顺时针旋转90°，得到△ABE′，连接E′D，使问题得到解决．请你参考小明的思路探究并解决下列问题：
    （1）猜想BD、DE、EC三条线段之间存在的数量关系式，并对你的猜想给予证明；
    （2）当动点E在线段BC上，动点D运动在线段CB延长线上时，如图2，其它条件不变，（1）中探究的结论是否发生改变？请说明你的猜想并给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    25、请阅读下列材料：
    问题：如图，在正方形ABCD和平行四边形BEFG中，点A，B，E在同一条直线上，P是线段DF的中点，连接PG，PC．
    探究：当PG与PC的夹角为多少度时，平行四边形BEFG是正方形？
    小聪同学的思路是：首先可以说明四边形BEFG是矩形；然后延长GP交DC于点H，构造全等三角形，经过推理可以探索出问题的答案．
    请你参考小聪同学的思路，探究并解决这个问题．
    （1）求证：四边形BEFG是矩形；
    （2）PG与PC的夹角为
    90
    度时，四边形BEFG是正方形．
    理由：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

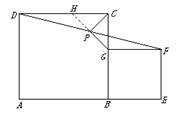
    （2011•临川区模拟）问题背景：如图1，四边形ABCD和CEFG都是正方形，B，C，E在同一条直线上，连接BG，DE．
    问题探究：
    （1）①如图1所示，当G在CD边上时，猜想线段BG、DE的数量关系及所在直线的位置关系．（不要求证明）
    ②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，请选择图2或图3证明你的判断．
    类比研究：
    （2）若将原题中的“正方形”改为“矩形”（如图4所示），且
    AB
    BC
    =
    CE
    CG
    =k（其中k＞0），请直接写出线段BG、DE的数量关系及位置关系．请选择图5或图6证明你的判断．
    拓展应用：
    （3）在（1）中图2中，连接DG、BE，若AB=3，EF=2，求BE2+DG2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    问题探究
    （1）如图1，△ABC是钝角三角形，∠C＞90°请在图1中，将△ABC补成矩形，使△ABC的两个顶点为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上．
    （2）如图2，△ABC是直角三角形，∠C=90°，AC=12，BC=5．请在图2中，将△ABC补成矩形，使得△ABC的两个顶点为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上，画出所有符合条件的矩形，并求此矩形的面积．
    问题解决
    （3）李大爷现有一个锐角三角形ABC（AB＞AC＞BC）形的鱼塘（如图3），鱼塘三个角的顶点A、B、C上各有一棵大树．现在李大爷想把原来的鱼塘扩建成一个矩形鱼塘（原鱼塘周围的面积足够大），并还想：三棵大树A、B、C中的两个为矩形鱼塘一边的两个端点，第三棵树落在鱼塘这一边的对边上．请你在图3中，画出所有符合条件的矩形鱼塘的示意图，并指出哪一个的周长最小？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    问题探究．
    用如图所示正方形纸板制作一个无盖的长方体盒子，可在正方体的四角减去相同的正方形，剩余部分即可做成一个无盖的长方体形盒子．
    （1）设正方形纸的边长为a，减去的小正方形的边长为x，请用a与x表示这个无盖长方体形盒子的容积；
    （2）把正方形的纸板换成长为a，宽为b的长方形纸板，怎样做一个无盖长方体形盒子？画图说明你的做法；
    （3）把（2）中做的长方体形盒子的容积用代数式表示出来；
    （4）比较（1）和（3）的结果，说说它们的区别和联系．

    查看答案和解析>>

    同步练习册答案