
【题目】如图,△ABC中,AB=AC=![]() ,cosC=
,cosC=![]() .
.

(1)动手操作:利用尺规作以AC为直径的⊙O,并标出⊙O与AB的交点D,与BC的交点E(保留作图痕迹,不写作法);
(2)综合应用:在你所作的图中,
①求证:弧DE=弧CE ;②求点D到BC的距离.
【答案】(1)作图见解析;(2)①证明见解析;②![]() .
.
【解析】试题分析:(1)先作出AC的中垂线,再画圆;
(2)边接AE,AE是BC的中垂线,∠DAE=∠CAE,得出 DE=CE,
(3)利用△BDE∽△BCA求出BD,再利用余弦求出BM,用勾股定理求出DM.
试题解析:(1)如图,
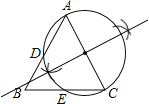
(2)如图,连接AE,
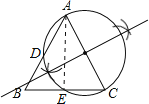
∵AC为直径,∴∠AEC=90°,
∵AB=AC,∴∠DAE=∠CAE,
∴ DE=CE .
(3)如图,连接AE,DE,作DM⊥BC交BC于点M,
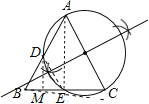
∵AC为直径,∴∠AEC=90°,
∵AB=AC= 4![]() ,cosC=
,cosC= ![]() ,∴EC=BE=4,∴BC=8,
,∴EC=BE=4,∴BC=8,
∵点A、D、E、C共圆,∴∠ADE+∠C=180°,
又∵∠ADE+∠BDE=180°,∴∠BDE=∠C,∴△BDE∽△BCA,
∴![]() 即BD
即BD![]() BA=BE
BA=BE![]() BC,∴BD×4
BC,∴BD×4![]() =4×8,
=4×8,
∴BD= ![]() ,
,
∵∠B=∠C,∴cos∠C=cos∠B=![]() ,
,
∴ ![]() ,∴BM=
,∴BM= ![]() ,
,
∴DM= ![]() .
.


科目:初中数学 来源: 题型:
【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
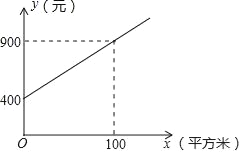
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )

A. (6,0) B. (6,3) C. (6,5) D. (4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得到△A′B′C′,请在图中画出△A′B′C′,并写出点A′、B′、C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(-4,n),B(2,-4)两点.
的图象交于A(-4,n),B(2,-4)两点.

(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)根据图象直接写出关于x的方程![]() 的解及不等式
的解及不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=a,CQ=![]() a 时,P、Q两点间的距离 (用含a的代数式表示).
a 时,P、Q两点间的距离 (用含a的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一列有理数-1,2,-3,4,-5,6,……,如图所示有序排列.根据图中的排列规律可知,“峰1” 中峰顶的位置(C的位置)是有理数4,那么,“峰5”中C 的位置是有理数 ,2017应排在A、E中 的位置.其中两个填空依次为

A.24 , AB.﹣24, AC.25, ED.﹣25, E
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com