
有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,
∠FDE=90°,DF=4,DE=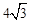 。将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上,现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动。
。将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上,现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动。
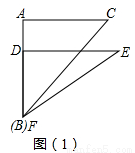
(1)如图(2),当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC= 度;
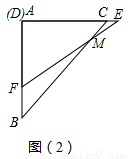
(2)如图(3),在三角板DEF运动过程中,当EF经过点C时,求FC的长;
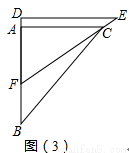
(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分面积为y,求y与x的函数解析式,并求出对应的x取值范围。
解:(1)15。
(2)如题图3所示,当EF经过点C时, 。
。
(3)在三角板DEF运动过程中,分三段讨论:
①当0≤x≤2时,如答图1所示,
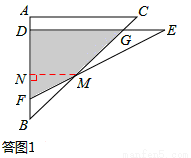
设DE交BC于点G.过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN。
又∵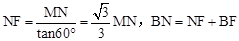 ,
,
∴NF+BF=MN,即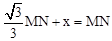 。
。
∴ 。
。
∴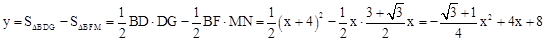 。
。
②当2<x≤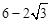 时,如答图2所示,
时,如答图2所示,
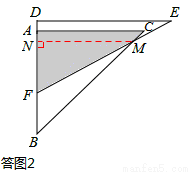
过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN。
又∵ ,
,
∴NF+BF=MN,即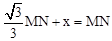 。
。
∴ 。
。
∴ 。
。
③当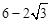 <x≤6时,如答图3所示,
<x≤6时,如答图3所示,
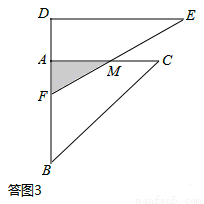
由BF=x,则AF=AB-BF=6-x,
设AC与EF交于点M,则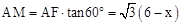 ,
,
∴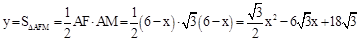 。
。
综上所述,y与x的函数解析式为:
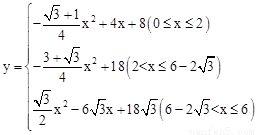 。
。
【解析】
试题分析:(1)如题图2所示,
∵在三角板DEF中,∠FDE=90°,DF=4,DE= ,
,
∴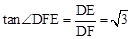 。∴∠DFE=60°。
。∴∠DFE=60°。
∴∠EMC=∠FMB=∠DFE-∠ABC=60°-45°=15°。
(2)如题图3所示,在Rt△ACF中,解直角三角形即可。
(3)认真分析三角板的运动过程,明确不同时段重叠图形的变化情况,分0≤x≤2,2<x≤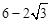 ,
,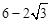 <x≤6三时段讨论:
<x≤6三时段讨论:
当0≤x≤2,即开始到DE与AC重合之前时,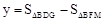 ;
;
当2<x≤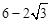 ,即DE与AC重合之后到EF经过点C之前时,
,即DE与AC重合之后到EF经过点C之前时,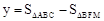 ;
;
当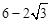 <x≤6,即EF经过点C之后到停止之前时,
<x≤6,即EF经过点C之后到停止之前时,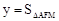 。
。


科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市南长区九年级上学期期末考试数学试卷(解析版) 题型:解答题
有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=4 ,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.

(1)如图(2),当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC= ?? 度;

(2)如图(3),在三角板DEF运动过程中,当EF经过点C时,求FC的长;

(3)在三角板DEF运动过程中,当D在BA的延长线上时,设BF=x,两块三角板重迭部分的面积为y.求y与x的函数关系式,并求出对应的x取值范围.
查看答案和解析>>
科目:初中数学 来源:2013年广东省汕头市中考数学试卷(解析版) 题型:解答题
 .将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
查看答案和解析>>
科目:初中数学 来源:2013年广东省中考数学试卷(解析版) 题型:解答题
 .将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com