
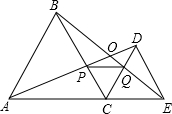
 CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:
CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论: ,推出△BCE和△CDE的面积相等,即可判断⑤.
,推出△BCE和△CDE的面积相等,即可判断⑤. ,
,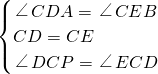 ,
, DE=
DE= AB,
AB,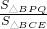 =
= ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 24、如图,C为线段AE上一动点,(不与A,E重合),在AE同侧分别作等边三角形ABC和CDE.则以下结论:①AD=BE ②CP=CQ ③AP=BQ ④DE=DP ⑤PQ∥AE中正确的有
24、如图,C为线段AE上一动点,(不与A,E重合),在AE同侧分别作等边三角形ABC和CDE.则以下结论:①AD=BE ②CP=CQ ③AP=BQ ④DE=DP ⑤PQ∥AE中正确的有查看答案和解析>>
科目:初中数学 来源: 题型:
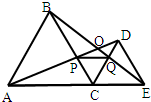 10、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )
10、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 15、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( )
15、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.
如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,C为线段AE上一动点(不与A,E重合)在AE同侧分别作等边△ABC和等边△CDE,AD与BE相交于点O,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.请你写出三个正确的结论:
如图,C为线段AE上一动点(不与A,E重合)在AE同侧分别作等边△ABC和等边△CDE,AD与BE相交于点O,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.请你写出三个正确的结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com