练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

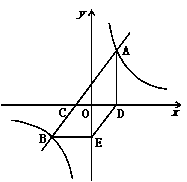
    如图，已知直线AB与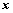轴交于点C，与双曲线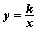交于A（3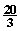，）、B（-5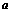，）两点.AD⊥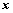轴于点D，BE∥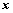轴且与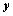轴交于点E.

    (1）求点B的坐标及直线AB的解析式；

    (2）判断四边形CBED的形状，并说明理由.


    解（1）∵双曲线过A（3，），∴.把B（-5，）代入,

    得. ∴点B的坐标是（-5，-4）. （3分）

           设直线AB的解析式为，

    将 A（3，）、B（-5，-4）代入得，

    ，    解得：.

    ∴直线AB的解析式为：.（6分）

    （2）四边形CBED是菱形.理由如下:

    点D的坐标是（3,0），点C的坐标是（-2,0）.

    ∵ BE∥轴，   ∴点E的坐标是（0,-4）.

    而CD =5， BE=5， 且BE∥CD.

    ∴四边形CBED是平行四边形. （8分）

    在Rt△OED中，ED2＝OE2＋OD2， ∴ ED＝＝5，∴ED＝CD.

    ∴□CBED是菱形. （10分）


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，菱形ABCD的顶点C的坐标为（-1，0），点B的坐标为（0，2），点A在第二象限．直线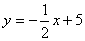与x轴、y轴分别交于点N、M．将菱形ABCD沿x轴向右平移m个单位，当点D落在△MON的内部时（不包括三角形的边），则m的值可能是（     ）

      A.1        B.2        C.4       D.8

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图(13)，AB是⊙O的切线，B为切点，圆心在AC上，∠A=,D为弧的中点.

    （1）求证：AB=BC

    （2）求证：四边形BOCD是菱形..

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     计算：sin30°++(1-π)=_____________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    为实施“农村留守儿童关爱计划”，某校对全校各班留守儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成了如下两幅不完整的统计图：

    (1）将该条形统计图补充完整；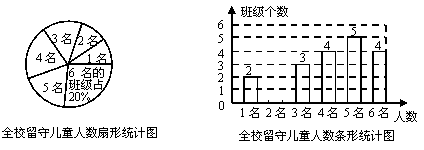

    (2）求该校平均每班有多少名留守儿童？

    (3）某爱心人士决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列运算正确的是

    A．a2＋a＝2a3　      　　　　　B．a3﹒a2＝a6　

    C．2a6÷a2＝2a3   　   　　　　D．(a2)4＝a8

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在矩形ABCD中，有一个菱形BFDE（点E、F分别在线段AB、CD上），记它们的面积分别为SABCD和SBFDE. 现给出下列命题：

    ①若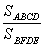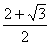＝，则tan∠EDF＝；

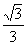    ②若DE2＝BD﹒EF，则DF＝2AD.

    那么，下面判断正确的是

    A．①是真命题，②是真命题 B．①是真命题，②是假命题

    C．①是假命题，②是真命题 D．①假命题，②假命题

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列各数中，最大的数是（   ）

      A．-2       B. 0       C.       D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     若a2+2ka+16是一个完全平方式，若k<0，则k =　         　．

     

    查看答案和解析>>

    同步练习册答案