练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    化简代数式，并判断当x满足不等式组时该代数式的符号．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2015-2016学年湖北省等七年级上第一次联考数学试卷（解析版） 题型：填空题

    毕达哥拉斯学派发明了一种“馨折形”填数法，如图所示，则“?”处应填_________．

    1

    2

    5

    3

    ?

    15

    7

    14

    35

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年浙江省杭州市5月中考模拟数学试卷（解析版） 题型：解答题

    在Rt△ABC中，∠ACB=90°，tan∠BAC=．点D在边AC上（不与A，C重合），连接BD，F为BD中点．

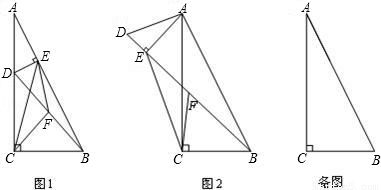
    （1）若过点D作DE⊥AB于E，连接CF、EF、CE，如图1．设CF=kEF，则k= ；

    （2）若将图1中的△ADE绕点A旋转，使得D、E、B三点共线，点F仍为BD中点，如图2所示．求证：BE-DE=2CF；

    （3）若BC=6，点D在边AC的三等分点处，将线段AD绕点A旋转，点F始终为BD中点，求线段CF长度的最大值．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年浙江省杭州市5月中考模拟数学试卷（解析版） 题型：选择题

    某校A、B两队10名参加篮球比赛的队员的身高（单位：cm）如下表所示：

    队员

    队

    1号

    2号

    3号

    4号

    5号

    A队

    176

    175

    174

    171

    174

    B队

    170

    173

    171

    174

    182

    设两队队员身高的平均数分别为，，身高的方差分别为SA2，SB2，则正确的选项是（ ）

    A．=，＞ B．＜，＜

    C．＞，＞ D．=，＜

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山东省威海市乳山市中考一模数学试卷（解析版） 题型：解答题

    如图，在△ABC中，AB=AC，以AB为直径作半圆⊙O，交BC于点D，连接AD．过点D作DE⊥AC，垂足为点E．

    （1）求证：DE是⊙O的切线；

    （2）求证：BD2=AB•CE．

    【答案】（1）证明见解析；（2）证明见解析.

    【解析】

    试题分析：（1）连接OD，AB为⊙0的直径得∠ADB=90°，由AB=AC，根据等腰三角形性质得AD平分BC，即DB=DC，则OD为△ABC的中位线，所以OD∥AC，而DE⊥AC，则OD⊥DE，然后根据切线的判定方法即可得到结论；

    （2）由∠B=∠C，∠CED=∠BDA=90°，得出△DEC∽△ADB，得出，从而求得BD•CD=AB•CE，由BD=AD，即可求得BD2=AB•CE．

    试题解析：（1）证明：连接OD，如图，

    ∵AB为⊙0的直径，

    ∴∠ADB=90°，

    ∴AD⊥BC，

    ∵AB=AC，

    ∴AD平分BC，即DB=DC，

    ∵OA=OB，

    ∴OD为△ABC的中位线，

    ∴OD∥AC，

    ∵DE⊥AC，

    ∴OD⊥DE，

    ∴DE是⊙0的切线；

    （2）证明：∵∠B=∠C，∠CED=∠BDA=90°，

    ∴△DEC∽△ADB，

    ∴，

    ∴BD•CD=AB•CE，

    ∵BD=AD，

    ∴BD2=AB•CE．

    考点：1.切线的判定；2.相似三角形的判定与性质．

    【题型】解答题
    【适用】一般
    【标题】2015届山东省威海市乳山市中考一模数学试卷（带解析）
    【关键字标签】
    【结束】
     

    如图1，将一个直角三角板的直角顶点P放在正方形ABCD的对角线BD上滑动，并使其一条直角边始终经过点A，另一条直角边与BC相交于点E．

    （1）求证：PA=PE；

    （2）若将（1）中的正方形变为矩形，其余条件不变（如图2），且AD=10，DC=8，求AP：PE；

    （3）在（2）的条件下，当P滑动到BD的延长线上时（如图3），请你直接写出AP：PE的比值．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山东省威海市乳山市中考一模数学试卷（解析版） 题型：填空题

    在一个不透明的袋子中，有3个白球和1个红球，它们只有颜色上的区别，从袋子中随机摸出一个球记下颜色放回，再随机地摸出一个球，则两次都摸到白球的概率为 ．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山东省威海市乳山市中考一模数学试卷（解析版） 题型：选择题

    如果a，b是一元二次方程x2-2x-4=0的两个根，那么a3b-2a2b的值为（ ）

    A．-8 B．8 C．-16 D．16

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年湖南省邵阳市邵阳县中考二模数学试卷（解析版） 题型：填空题

    如图，已知AB∥CD，EF平分∠AEG，∠EFG=50°，则∠EGF的度数是 ．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年广西省南宁市西乡塘区中考二模数学试卷（解析版） 题型：选择题

    在实数0，-π，，-4中，最小的数是（ ）

    A．0 B．-π C． D．-4

    查看答案和解析>>

    同步练习册答案