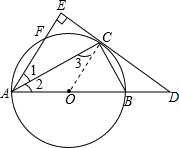
(1)DE是⊙O的切线
证明:连接OC(如图)
∵
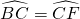
,∴∠1=∠2
∵⊙O是△ABC的外接圆
∴点C在圆上
∴OC=OA
∴∠3=∠2
∴∠3=∠1
∴OC∥AE
∵AE⊥DE,∴∠AED=90°
∴∠OCD=90°
∴OC⊥DC,即OC⊥DE
∴DE是⊙O的切线
(2)解:在△ADE中,由(1)知OC∥AE
∴

设OC=t
∵
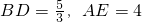
∴
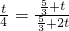
整理,得6t
2-7t-20=0
解得
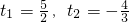
经检验t
1,t
2均为原方程的解,由于线段长为非负,故舍去负值.
得

∴AB=5
∵DC切⊙O于点C,DBA是⊙O的割线
∴
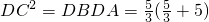
∴
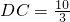
∵∠BCD=∠2,∠D是公共角,
∴△DBC∽△DCA
∴
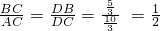
由已知AB是⊙O的直径
∴∠ACB=90°,∴
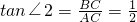
∴
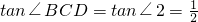
分析:(1)DE是⊙O的切线,连接OC,根据题意得∠1=∠2,∠3=∠2,则∠3=∠1,从而得出OC∥AE,根据AE⊥DE得出OC⊥DE,则DE是⊙O的切线;
(2)由OC∥AE,得

,设OC=t,代入即可得出t的值,即可求出CO,AB,再由切割线定理得出CD,则可证明△DBC∽△DCA,得出比例式BC:AC,根据∠BCD=∠2
即可得出∠BCD的正切值.
点评:本题是一道综合题目,考查了切线的判定和性质、相似三角形的判定和性质、平行线分线段成比例,解直角三角形,是中考压轴题.

 的延长线于E,交⊙O于点F,且
的延长线于E,交⊙O于点F,且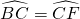
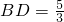 ,AE=4,求∠BCD的正切值.
,AE=4,求∠BCD的正切值. (1)DE是⊙O的切线
(1)DE是⊙O的切线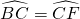 ,∴∠1=∠2
,∴∠1=∠2
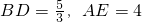
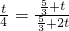
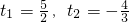

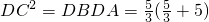
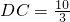
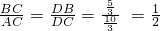
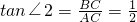
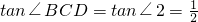
 ,设OC=t,代入即可得出t的值,即可求出CO,AB,再由切割线定理得出CD,则可证明△DBC∽△DCA,得出比例式BC:AC,根据∠BCD=∠2
,设OC=t,代入即可得出t的值,即可求出CO,AB,再由切割线定理得出CD,则可证明△DBC∽△DCA,得出比例式BC:AC,根据∠BCD=∠2

 如图,已知A是半径为1的⊙O上一点,以A为圆心,AO为半径画弧交⊙O于点B、C;以C为圆心,CO为半径画弧交⊙O于点D、A.则图中阴影面积为
如图,已知A是半径为1的⊙O上一点,以A为圆心,AO为半径画弧交⊙O于点B、C;以C为圆心,CO为半径画弧交⊙O于点D、A.则图中阴影面积为 (2012•梁子湖区模拟)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(2012•梁子湖区模拟)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
 (2012•资阳)已知a、b是正实数,那么,
(2012•资阳)已知a、b是正实数,那么, (2012•河池)如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
(2012•河池)如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.