练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AD是△ABC的高，BE平分∠ABC交AD于E，若∠C=70°，∠BED=64°，求∠BAC的度数．

    【答案】58°

    在直角三角形ABD中，

    ,

    因为BE平分∠ABC，所以°，则∠BAC=180-70-52=58°。

    【解析】试题分析：由已知条件，首先得出∠DAC=20°，再利用∠ABE=∠EBD，进而得出∠ABE+∠BAE=64°，求出∠EBD=26°，进而得出答案．

    解：∵AD是△ABC的高，∠C=70°，

    ∴∠DAC=20°，

    ∵BE平分∠ABC交AD于E，

    ∴∠ABE=∠EBD，

    ∵∠BED=64°，

    ∴∠ABE+∠BAE=64°，

    ∴∠EBD+64°=90°，

    ∴∠EBD=26°，

    ∴∠BAE=38°，

    ∴∠BAC=∠BAE+∠CAD=38°+20°=58°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中,∠C=90°,AC=3,BC=4,D是AB上一动点（不与A、B重合）,DE⊥AC于点E,DF⊥BC于点F,点D由A向B移动时,矩形DECF的周长变化情况是（ ）

    A. 逐渐减小 B. 逐渐增大 C. 先增大后减小 D. 先减小后增大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图8，四边形ABEG、GEFH、HFCD都是边长为1的正方形.

    （1）求证：△AEF∽△CEA；

    （2）求证：∠AFB+∠ACB=45°.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，连接BD，CE，BD和CE相交于点F，若△ABC不动，将△ADE绕点A任意旋转一个角度．

    （1）求证：△BAD≌△CAE．

    （2）如图①，若∠BAC=∠DAE=90°，判断线段BD与CE的关系，并说明理由；

    （3）如图②，若∠BAC=∠DAE=60°，求∠BFC的度数；

    （4）如图③，若∠BAC=∠DAE= ，直接写出∠BFC的度数（不需说明理由）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】尺规作图：某学校正在进行校园环境的改造工程设计，准备在校内一块四边形花坛内栽上一棵桂花树．如图，要求桂花树的位置（视为点P），到花坛的两边AB、BC的距离相等，并且点P到点A、D的距离也相等．请用尺规作图作出栽种桂花树的位置点P（不写作法，保留作图痕迹）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知三角形的两边a＝3，b＝7，则下列长度的四条线段中能作为第三边c的是（　　）
    A.3
    B.4
    C.7
    D.10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

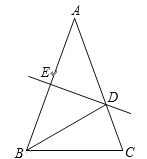
    【题目】如图，在△ABC中，DE是边AB的垂直平分线，交AB于E、交AC于D，连接BD．

    （1）若∠ABC＝∠C，∠A＝40°，求∠DBC的度数；

    （2）若AB＝AC，且△BCD的周长为18cm，△ABC的周长为30cm，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】尺规作图作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA，OB于C，D，再分别以点C，D为圆心，以大于CD长为半径画弧，两弧交于点P，作射线OP．由作法得△OCP≌△ODP的根据是（ ）

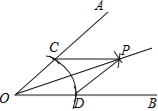
    A. SAS B. ASA C. AAS D. SSS

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】地球半径约为6 400 000m，这个数字用科学记数法表示为m．

    查看答案和解析>>

    同步练习册答案