
 ��֪������������
��֪������������ ��ͼ���ڵ�һ���ķ�֧����n����A1��1��y1����A2��2��y2��������An��n��yn������ֱ��A1A2�Ľ���ʽΪy=k1x+b1��A2A3�Ľ���ʽΪy=k2x+b2������AnAn+1�Ľ���ʽΪy=knx+bn��
��ͼ���ڵ�һ���ķ�֧����n����A1��1��y1����A2��2��y2��������An��n��yn������ֱ��A1A2�Ľ���ʽΪy=k1x+b1��A2A3�Ľ���ʽΪy=k2x+b2������AnAn+1�Ľ���ʽΪy=knx+bn�� ��
�� ����
���� ������y=k1x+b1��
������y=k1x+b1�� ��
�� -1=-
-1=- ��
�� ��
�� ��
�� ������A3��������3��
������A3��������3�� ������A4��������4��
������A4��������4�� ����
���� -
- ��k3=
��k3= -
- ��
�� -1+
-1+ -
- +
+ -
- =-1+
=-1+ =-
=- ��
�� ��
�� ��
�� ������A3��������3��
������A3��������3�� ������A4��������4��
������A4��������4�� ����������A20������20��
����������A20������20��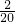 ������A21������21��
������A21������21��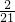 ����
���� -
- ��k2=
��k2= -
- ��k3=
��k3= -
- ������k20=
������k20=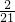 -
-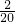 ��
�� -
- +
+ -
- +
+ -
- +��+
+��+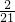 -
-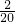 =-2+
=-2+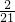 =-
=-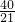 ��
�� ������A3��������3��
������A3��������3�� ������A4��������4��
������A4��������4�� ����������An������n��
����������An������n�� ������An+1������n+1��
������An+1������n+1��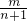 ����
���� -m��k2=
-m��k2= -
- ��k3=
��k3= -
- ������kn=
������kn=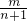 -
- ��
�� -m+
-m+ -
- +
+ -
- +��+
+��+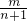 -
- =-m+
=-m+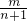 =-
=-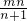 ��
�� ��ȷ����A1������Ϊ��1��1������A2������Ϊ��2��
��ȷ����A1������Ϊ��1��1������A2������Ϊ��2�� �����ٰ����Ǵ���y=k1x+b1�õ�k1+b1=1�٣�2k1x+b1=
�����ٰ����Ǵ���y=k1x+b1�õ�k1+b1=1�٣�2k1x+b1= �ڣ�Ȼ���â�-�ٿ����k1=
�ڣ�Ȼ���â�-�ٿ����k1= -1=-
-1=- ��
�� ����ȷ����A1������Ϊ��1��1������A2������Ϊ��2��
����ȷ����A1������Ϊ��1��1������A2������Ϊ��2�� ������A3������Ϊ��3��
������A3��������3�� ������A4��������4��
������A4������Ϊ��4�� �����루1��һ���õ�k2=
�����루1��һ���õ�k2= -
- ��k3=
��k3= -
- ���õ�k1+k2+k3��ֵ��
���õ�k1+k2+k3��ֵ�� ����ȷ����A1����Ϊ��1��2������A2����Ϊ��2��
����ȷ����A1����Ϊ��1��2������A2����Ϊ��2�� ������A3������Ϊ��3��
������A3��������3�� ������A4��������4��
������A4��������4�� ����������A20������20��
����������A20������20��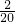 ������A21������21��
������A21����Ϊ��21��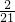 �������գ�1���õ�k1=
�������գ�1���õ�k1= -
- ��k2=
��k2= -
- ��k3=
��k3= -
- ������k20=
������k20=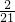 -
-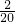 ����k1+k2+k3+��+k20=
����k1+k2+k3+��+k20= -
- +
+ -
- +
+ -
- +��+
+��+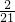 -
-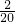 ��Ȼ����мӼ����㼴�ɣ�
��Ȼ����мӼ����㼴�ɣ� ������A3������Ϊ��3��
������A3��������3�� ������A4��������4��
������A4��������4�� ����������An������n��
����������An������n�� ������An+1������n+1��
������An+1����Ϊ��n+1��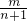 ������ͬ���ɵõ�k1=
������ͬ���ɵõ�k1= -m��k2=
-m��k2= -
- ��k3=
��k3= -
- ������kn=
������kn=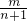 -
- ����k1+k2+k3+��+kn=
����k1+k2+k3+��+kn= -m+
-m+ -
- +
+ -
- +��+
+��+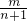 -
- ��Ȼ����з�ʽ�ļӼ����㼴�ɣ�
��Ȼ����з�ʽ�ļӼ����㼴�ɣ�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A��1�� | B��2�� | C��3�� | D��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| x |
| 1 |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com