
 ∠DAB=40°,∠ADC=100°,即可得△ADF≌△ABF,则∠ADF=∠ABF;又因为EF是AB的垂直平分线,所以AF=BF,所以∠ABF=∠BAF=40°,即可求得∠CDF的度数.
∠DAB=40°,∠ADC=100°,即可得△ADF≌△ABF,则∠ADF=∠ABF;又因为EF是AB的垂直平分线,所以AF=BF,所以∠ABF=∠BAF=40°,即可求得∠CDF的度数.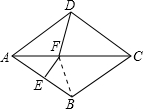 解:∵四边形ABCD是菱形,∠DAB=80°,
解:∵四边形ABCD是菱形,∠DAB=80°, ∠DAB=40°,∠ADC=100°,
∠DAB=40°,∠ADC=100°,

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:
 如图,菱形ABCD的对角线AC和BD相交于O点,E,F,G,H分别是AB,BC,CD,DA的中点,求证:E,F,G,H四个点在以O为圆心的同一个圆上.
如图,菱形ABCD的对角线AC和BD相交于O点,E,F,G,H分别是AB,BC,CD,DA的中点,求证:E,F,G,H四个点在以O为圆心的同一个圆上.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| DM |
| 1 |
| DN |
查看答案和解析>>
科目:初中数学 来源: 题型:
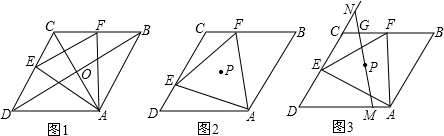
 如图,菱形ABCD的边长为4,点P1在AB边上,且AP1=3.在BC边上截取BP2=AP1,得点P2;在CD边上截取CP3=BP2,得点p3;在DA边上截取DP4=CP3,得点p4;在AB边上截取AP5=DP4,得点P5;…,按此作法进行下去,则点p2011( )
如图,菱形ABCD的边长为4,点P1在AB边上,且AP1=3.在BC边上截取BP2=AP1,得点P2;在CD边上截取CP3=BP2,得点p3;在DA边上截取DP4=CP3,得点p4;在AB边上截取AP5=DP4,得点P5;…,按此作法进行下去,则点p2011( )查看答案和解析>>
科目:初中数学 来源: 题型:
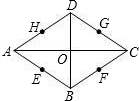 如图,菱形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是它的四条边AB、BC、CD、DA的中点,E、F、G、H四个点共圆吗?(友情提示:要找到一点,证明这四点到找到的这点(圆心)的距离相等即可)
如图,菱形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是它的四条边AB、BC、CD、DA的中点,E、F、G、H四个点共圆吗?(友情提示:要找到一点,证明这四点到找到的这点(圆心)的距离相等即可)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com