
 动到终点时,两个动点都停止运动.
动到终点时,两个动点都停止运动.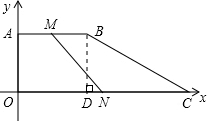 解:(1)作BD⊥OC于D,
解:(1)作BD⊥OC于D,| BC2-CD2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
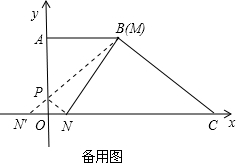 此时PM+PN=PM+PN′=MN′长度最小.
此时PM+PN=PM+PN′=MN′长度最小.
|
|
| 3 |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
| 3 |
| 4 |


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
 如图,已知直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于E和F.
如图,已知直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于E和F.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,已知直角梯形OABC,BC∥OA,A(20,0),C(0,4
如图,在平面直角坐标系中,已知直角梯形OABC,BC∥OA,A(20,0),C(0,4| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 果存在,求出t的值;如果不存在,请说明理由.
果存在,求出t的值;如果不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:第27章《二次函数》中考题集(28):27.3 实践与探索(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com