Question

5．如图，流经某市的一条河流的两岸互相平行，河岸l₁上有一排观赏灯，已知相邻两灯之间的距离AB=10米，某人在河岸l₂的C处测得∠ACE=60°，然后沿河岸向右走了90米到达D处，测得∠BDC=30°．求河流的宽度．（结果精确到0.1米，参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）

Answer 1

分析 过点A作AF∥BD交l₂于点F．利用l₁∥l₂，AF∥DB，得到四边形AFDB是平行四边形，利用平行四边形的性质得到DF=AB=10，∠AFC=30°从而得到CF=CD-DF=90-10=80，然后利用∠ACE是△ACF的一个外角，得∠CAF=∠ACE-∠AFC=60°-30°=30°，得到进而AC=CF=80．然后在Rt△AEC中求得AE的长即可．

解答 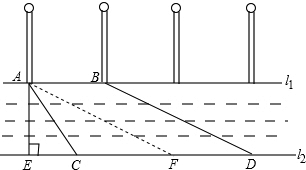解：过点A作AF∥BD交l₂于点F．
∵l₁∥l₂，AF∥DB，
∴四边形AFDB是平行四边形．
∴DF=AB=10，∠AFC=30°，
∴CF=CD-DF=90-10=80．
又∵∠ACE是△ACF的一个外角，
∴∠CAF=∠ACE-∠AFC=60°-30°=30°，
∴∠CAF=∠AFC．
∴AC=CF=80．
在Rt△AEC中，∠ACE=60°
∴AE=AC•sin60°=80×$\frac{\sqrt{3}}{2}$≈69.28≈69.3（米）．
答：河流的宽度AE约为69.3米．

点评 本题考查了解直角三角形的应用，规则图形可以通过作平行线转化为平行四边形与直角三角形的问题进行解决．