解:①将方程移项,并化系数为1得:x
2=
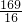
,
解得:x=±

;
②原式=4-5-

-0.2+1
=
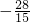
;
③原式=(2-1)(2+1)(2
2+1)(2
4+1)(2
8+1)(2
16+1)(2
32+1)+1,
=(2
2-1)(2
2+1)(2
4+1)(2
8+1)(2
16+1)(2
32+1)+1,
=(2
4-1)(2
4+1)(2
8+1)(2
16+1)(2
32+1)+1,
=(2
32-1)(2
32+1)+1,
=2
64-1+1
=2
64.
分析:①将x
2当做一个整体,继而进行开平方运算即可得出答案.
②分别进行开平方、开立方、二次根式的化简、零指数幂的运算,然后合并可得出答案.
③分析式子中2,2
2,2
4,每一个数都是前一个数的平方,若在(2+1)前面有一个(2-1),就可以连续递进地运用(a+b)(a-b)=a
2-b
2了.
点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式等考点的运算;同时考查了平方差公式的运用,构造能使用平方差公式的条件是解题的关键.

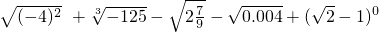
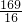 ,
, ;
; -0.2+1
-0.2+1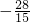 ;
;

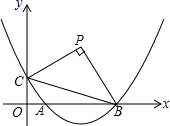 如图,已知抛物线y=
如图,已知抛物线y=