
分析 过P作y轴的平行线,交AC于Q;易求得直线AB的解析式,可设出P点的坐标,进而可表示出P、Q的纵坐标,也就得出了PQ的长;然后根据三角形面积的计算方法,可得出关于△PAB的面积与P点横坐标的函数关系式,根据所得函数的性质即可求出△PAB的最大面积及对应的P点坐标.
解答  解:如图,过点P作平行于y轴的直线交AB于点Q;
解:如图,过点P作平行于y轴的直线交AB于点Q;
∵A(0,3),B(6,0),
∴AB的解析式为y=-$\frac{1}{2}$x+3;
设P点的坐标为(m,$\frac{1}{4}$m2-2m+3),
则Q点的坐标为(m,-$\frac{1}{2}$m+3);
∴PQ=-$\frac{1}{2}$m+3-($\frac{1}{4}$m2-2m+3)=-$\frac{1}{4}$m2+$\frac{3}{2}$m.
∵S△PAB=S△PAQ+S△PCQ=$\frac{1}{2}$×(-$\frac{1}{4}$m2+$\frac{3}{2}$m)×6
=-$\frac{3}{4}$(m-3)2+$\frac{27}{4}$;
∴当m=3时,△PAB的面积最大为$\frac{27}{4}$;
此时,P点的坐标为(3,-$\frac{3}{4}$).
点评 此题考查了二次函数图象上点的坐标特征、二次函数的最值、图形面积的求法等知识.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
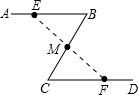 如图、公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E,F,M,且BE=CF,M在BC的中点,试判断三只石凳E,M,F恰好在一直线上吗?为什么?
如图、公园里有一条“Z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小石凳E,F,M,且BE=CF,M在BC的中点,试判断三只石凳E,M,F恰好在一直线上吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
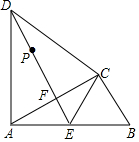 如图,在△ABC中,∠ACB=90°,以AC为底边作等腰三角形△ACD,AD=CD,E为AB的中点,连接CE、DE,DE与AC相交于点F.
如图,在△ABC中,∠ACB=90°,以AC为底边作等腰三角形△ACD,AD=CD,E为AB的中点,连接CE、DE,DE与AC相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
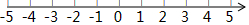 结合数轴与绝对值的知识回答下列问题:
结合数轴与绝对值的知识回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
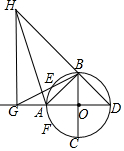 设AD、BC是圆O的互相垂直的直径,E和F分别在劣弧$\widehat{AB}$,$\widehat{CA}$上,若$\widehat{AE}$和$\widehat{AF}$相等,直线DA和直线BE的交点为G,直线FA和直线DB的交点为H,求证:∠HGA是直角.
设AD、BC是圆O的互相垂直的直径,E和F分别在劣弧$\widehat{AB}$,$\widehat{CA}$上,若$\widehat{AE}$和$\widehat{AF}$相等,直线DA和直线BE的交点为G,直线FA和直线DB的交点为H,求证:∠HGA是直角.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com