
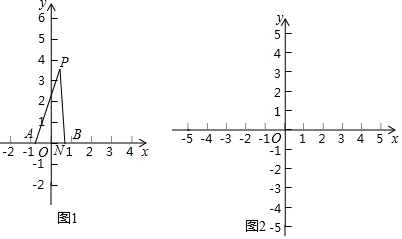
���� ��1��D��F���߶�AB�ġ������㡱��ֻҪ֤����AEB��30�㣬��ADB��30�㼴�ɣ�
��2������ͼ2�У���M��A�غ�ʱ���ɵ�MN����Сֵ������ͼ3�У���N��B�غ�ʱ���ɵ�MN�����ֵ����MH��PB��H����MH=x����PM=2x��PH=$\sqrt{3}$x���ֱ����MN��ֵ���ɽ�����⣻
��3����ͼ4�У����ȱ������Ρ�ADB����DΪԲ��DAΪ�뾶����D������D��HG�����ڵ�Pʱ����֪��ʱ��APB=30�㣬�����ʱt��ֵ���ɣ�
��� �⣺��1����ͼ1�У��߶�AB�ġ������㡱��E��D��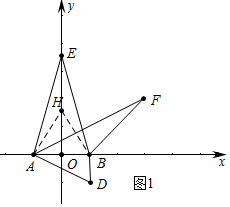
��D��1��-1����E��3��2����F��0��2+$\sqrt{3}$������֪��ABF=135�㣬
�ڡ�ABF�У�BF=2$\sqrt{2}$��AB=2��
��BF��AB��
���BAF����F��
���F��22.5�㣬��F��ʾ�߶�AB�ġ������㡱��
��tan��D=2��$\frac{\sqrt{3}}{3}$��
���D��30�㣬��D���߶�AB�ġ������㡱��
ȡH��0��$\sqrt{3}$������AH=AB=HB=EH=2��
���AHB�ǵȱ������Σ�
���AHB=60�㣬��AHO=��BHO=30�㣬
���HAE=��HEA=��HBE=��HEB=15�㣬
���AEB=30�㣬��E���߶�AB�ġ������㡱��
�ʴ�ΪD��F��
��2������ͼ2�У���M��A�غ�ʱ���ɵ�MN����Сֵ��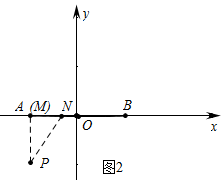
��Rt��APN�У��ߡ�P=30��AP=2����PAN=90�㣬
��AN=AP•tan30��=$\frac{2\sqrt{3}}{3}$��
����ͼ3�У���N��B�غ�ʱ���ɵ�MN�����ֵ����MH��PB��H����MH=x����PM=2x��PH=$\sqrt{3}$x��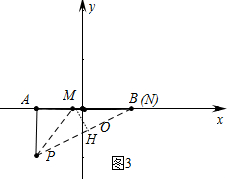
��֪��AM=$\sqrt{4{x}^{2}-1}$��BM=2-$\sqrt{4{x}^{2}-1}$��BH=$\sqrt{5}$-$\sqrt{3}$x��
��Rt��BMH����MH2+BH2=BM2��
��x2+��$\sqrt{5}$-$\sqrt{3}$x��2=[2-$\sqrt{4{x}^{2}-1}$]2��
���x=2$\sqrt{5}$-$\sqrt{15}$��
��BM=2-$\sqrt{4{x}^{2}-1}$=2-��5$\sqrt{3}$-8��=10-5$\sqrt{3}$��
��MN�ķ�ΧΪ$\frac{2\sqrt{3}}{3}$��MN��10-5$\sqrt{3}$��
��3����ͼ4�У����ȱ������Ρ�ADB����DΪԲ��DAΪ�뾶����D������D��HG�����ڵ�Pʱ����֪��ʱ��APB=30�㣬�����ʱt��ֵ���ɣ�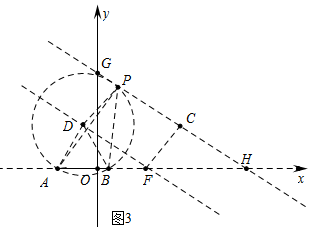
��OF��HG��x����F����FC��HG��C��
��ֱ��GH�Ľ���ʽΪy=-$\frac{1}{2}$x+4��
��sin��FCH=$\frac{FC}{FH}$=$\frac{OG}{GH}$��
��$\frac{2}{FH}$=$\frac{4}{4\sqrt{5}}$��
��FH=2$\sqrt{5}$��
��F��8-2$\sqrt{5}$��0����
��ֱ��DF�Ľ���ʽΪy=-$\frac{1}{2}$x+4-$\sqrt{5}$��
�ߵ�D��������Ϊ$\sqrt{3}$��
y=$\sqrt{3}$ʱ��$\sqrt{3}$=-$\frac{1}{2}$x+4-$\sqrt{5}$��
��x=8-2$\sqrt{5}$-2$\sqrt{3}$��
��D��8-2$\sqrt{5}$-2$\sqrt{3}$��$\sqrt{3}$����
��A��t-1��0����B��t+1��0����
��t=8-2$\sqrt{5}$-2$\sqrt{3}$��
�۲�ͼ���֪��t��8-2$\sqrt{5}$-2$\sqrt{3}$ʱ���߶�AB�����С������㡱����ֱ��GH�·�
���� ���⿼����һ�κ����ۺ��⡢�ȱ������ε��ж������ʡ�������Ǻ���������ϵ��������ֱ�������Σ�ֱ��������30�Ƚ����ʵ�֪ʶ������Ĺؼ����������⣬ѧ��ȡ����㣬����λ�ý�����⣬ѧ���÷������۵�˼��˼�����⣬ѧ�����Ӹ���Բ������⣬�����п�ѹ���⣮


 ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д� �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д� Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д� ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д� �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
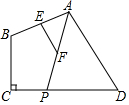 ��ͼ����֪�ı���ABCD�У���C=90�㣬��P��CD���ϵĶ��㣬����AP��E��F�ֱ���AB��AP���е㣬����P��CD�ϴӵ�D���C�ƶ������У����н��۳������ǣ�������
��ͼ����֪�ı���ABCD�У���C=90�㣬��P��CD���ϵĶ��㣬����AP��E��F�ֱ���AB��AP���е㣬����P��CD�ϴӵ�D���C�ƶ������У����н��۳������ǣ�������| A�� | �߶�EF�ij��ȼ�С������ | B�� | �߶�EF�ij����� | ||
| C�� | �߶�EF�ij������� | D�� | �߶�EF�ij���С |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1 | B�� | ��$\sqrt{2}$ | C�� | ��$\sqrt{3}$ | D�� | ��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{{\begin{array}{l}{k=-1}\\{b=1}\end{array}}\right.$ | B�� | $\left\{{\begin{array}{l}{k=-1}\\{b=0}\end{array}}\right.$ | C�� | $\left\{\begin{array}{l}k=1\\ b=2\end{array}\right.$ | D�� | $\left\{\begin{array}{l}k=1\\ b=-4\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
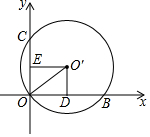 ��ͼ����ƽ��ֱ������ϵ�У���O�侭��ԭ��O�����ҷֱ���x�ᡢy�ύ�ڵ�B��C���ֱ���O��E��OC�ڵ�E��O��D��OB�ڵ�D����OB=8��OC=6�����O��İ뾶Ϊ��������
��ͼ����ƽ��ֱ������ϵ�У���O�侭��ԭ��O�����ҷֱ���x�ᡢy�ύ�ڵ�B��C���ֱ���O��E��OC�ڵ�E��O��D��OB�ڵ�D����OB=8��OC=6�����O��İ뾶Ϊ��������| A�� | 7 | B�� | 6 | C�� | 5 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 21�棬20�� | B�� | 21�棬26�� | C�� | 22�棬20�� | D�� | 22�棬26�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com