
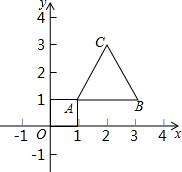 如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为(-2014,$\sqrt{3}$+1).
如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为(-2014,$\sqrt{3}$+1). 分析 据轴对称判断出点A变换后在x轴上方,然后求出点A纵坐标,再根据平移的距离求出点A变换后的横坐标,最后写出即可.
解答 解:解:∵△ABC是等边三角形AB=3-1=2,
∴点C到x轴的距离为1+2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$+1,
横坐标为2,
∴C(2,$\sqrt{3}$+1),
第2016次变换后的三角形在x轴上方,
点C的纵坐标为$\sqrt{3}$+1,
横坐标为2-2016×1=-2014,
所以,点C的对应点C′的坐标是(-2014,$\sqrt{3}$+1),
故答案为:(-2014,$\sqrt{3}$+1).
点评 本题考查了坐标与图形变化-平移,等边三角形的性质,读懂题目信息,确定出连续2016次这样的变换得到三角形在x轴上方是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 同位角相等 | |
| B. | 和为180°的两个角互为邻补角 | |
| C. | 经过直线外一点,有且只有一条直线与这条直线平行 | |
| D. | 相等的角是对顶角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将矩形ABCD折叠使点A,C重合,折痕交BC于点E,交AD于点F,可以得到四边形AECF是一个菱形,若AB=4,BC=8,求菱形AECF的面积.
将矩形ABCD折叠使点A,C重合,折痕交BC于点E,交AD于点F,可以得到四边形AECF是一个菱形,若AB=4,BC=8,求菱形AECF的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
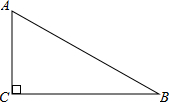 如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | 4 | C. | 8$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 每批粒数 | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
| 发芽粒数 | 96 | 282 | m | 570 | 948 | 1912 | 2850 |
| 发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | n | 0.950 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com