练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若（x-3）（x+m）=x2+nx-15，求
    n2-m2
    8n+5
    的值．
    考点：多项式乘多项式
    专题：计算题
    分析：首先把）（x-3）（x+m）利用多项式的乘法公式展开，然后根据多项式相等的条件：对应项的系数相同即可得到m、n的值，从而求解．
    解答：解：（x-3）（x+m）
    =x2+（m-3）x-3m
    =x2+nx-15，
    则
    m-3=n
    -3m=-15

    解得：
    m=5
    n=2
    ．
    n2-m2
    8n+5
    =
    22-52
    8×2+5
    =-1    ．
    点评：本题考查了多项式的乘法法则以及多项式相等的条件，理解多项式的乘法法则是关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    下列运算正确的是（　　）
    A、（ab3）2=a2b6
    B、（x-2）（x-3）=x2-6
    C、（x-2）2=x2-4
    D、2a×3a=6a

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如果我们定义：“到三角形的两个顶点距离相等的点，叫做此三角形的开心点．”那么：
    （1）如图1，观察并思考，△ABC的开心点有
     
    个；
    （2）如图2，CD为等边三角形ABC的高，开心点P在高CD上，且PD=
    1
    2
    AB，则∠APB的度数为
     
    ；
    （3）已知△ABC为直角三角形，斜边BC=5，AB=3，开心点P在AC边上，试探究PA的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （3x-2）2-5（3x-2）+4=0．

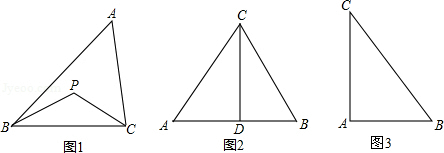
    查看答案和解析>>

    科目：初中数学 来源： 题型：

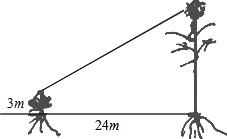    有一只喜鹊在一棵3m高的小树上觅食，它的巢筑在距离该树24m的一棵大树上，大树高14m，且巢离树顶部1m．当它听到巢中幼鸟的叫声，立即赶过去，如果它飞行的速度为5.2m/s，那它至少需要多少时间才能赶回巢中？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）
    x
    4
    -y=-1
    x+4y=4
    （用加减消元法）          
    （2）
    x+y=25
    2x-y=8
    （用代入消元法）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

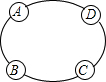    如图是某汽车维修公司的维修点在环形公路上的分布图．公司在年初分配给A，B，C，D四个维修点某种配件各50件．在使用前发现需将A，B，C，D四个维修点的这批配件分别调整为40，45，54，61件，但调整只能在相邻维修点之间进行，那么要完成上述调整，最少的调动件次为多少？说明理由．（注：n件配件从一个维修点调整到相邻维修点的调动件次为n）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

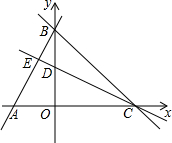    如图，在坐标平面中，直线y=2x+12分别交x轴、y轴于A、B，把△AOB绕点O旋转，使点B落在x轴正半轴点C处，A落在y轴上点D处，直线CD于AB相交于点E．
    （1）求直线CD的解析式；
    （2）点P为线段CD上一点，过点P坐x轴的平行线交直线BC于F，设P点的横坐标为m，△PDF的面积为S平方单位，求S与m的函数关系式；
    （3）在（2）的条件下，若△PCF与△BCP相似，求P点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

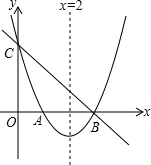    如图，直线y=-x+3与x轴，y轴分别相交于点B，点C，经过B、C两点的抛物线y=ax2+bx+c（a≠0）与x轴的另一交点为A，顶点为P，且对称轴是直线x=2．
    （1）求A点的坐标及该抛物线的函数表达式；
    （2）求出△PBC的面积；
    （3）请问在对称轴x=2右侧的抛物线上是否存在点Q，使得以点A、B、C、Q所围成的四边形面积是△PBC的面积的
    91
    72
    ？若存在，请求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案