
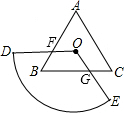
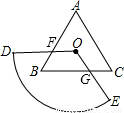
 如图,扇形ODE的圆心角为120°,正三角形ABC的中心恰好为扇形ODE的圆心,且点B在扇形ODE内
如图,扇形ODE的圆心角为120°,正三角形ABC的中心恰好为扇形ODE的圆心,且点B在扇形ODE内 .
.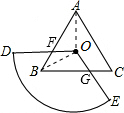 证明:(1)如图,连接OA、OB,设OD交AB于F,OE交BC于G,
证明:(1)如图,连接OA、OB,设OD交AB于F,OE交BC于G,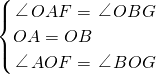 ,
, .
. ;
; S△ABC,
S△ABC, ,
, .
. ,可以先从三角形考虑,O为中心也就是与正三角形的中心角重合,所以应为120°,证明是要分两种情况:即特殊和一般,特殊情况时就是猜想所用的情况,显然成立,一般情况的证明从三角形全等把四边形的面积分解成两个三角形,最后再归到正三角形的中心角为120°的三角形.
,可以先从三角形考虑,O为中心也就是与正三角形的中心角重合,所以应为120°,证明是要分两种情况:即特殊和一般,特殊情况时就是猜想所用的情况,显然成立,一般情况的证明从三角形全等把四边形的面积分解成两个三角形,最后再归到正三角形的中心角为120°的三角形.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
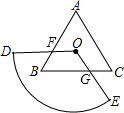 如图,扇形ODE的圆心角为120°,正三角形ABC的中心恰好为扇形ODE的圆心,且点B在扇形ODE内
如图,扇形ODE的圆心角为120°,正三角形ABC的中心恰好为扇形ODE的圆心,且点B在扇形ODE内| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,扇形AOB的圆心角为90°,四边形OCDE是边长为1的正方形,点C、E、D分别在OA、OB、AB上,过A作AF⊥ED交ED的延长线于点F,那么图中阴影部分的面积为
如图,扇形AOB的圆心角为90°,四边形OCDE是边长为1的正方形,点C、E、D分别在OA、OB、AB上,过A作AF⊥ED交ED的延长线于点F,那么图中阴影部分的面积为查看答案和解析>>
科目:初中数学 来源:2005年四川省广元市中考数学试卷(解析版) 题型:解答题
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com