
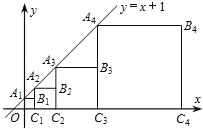
【题目】如图,直线 y=x+1 与 y 轴交于点 A1,以 OA1为边,在 y 轴右侧作正方形 OA1B1C1,延长 C1B1交直线 y=x+1 于点 A2,再以 C1A2为边作正方形,…,这些正方形与直线 y=x+1 的交点分别为 A1,A2,A3,…,An,则点 Bn 的坐标为_______.
科目:初中数学 来源: 题型:
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD= ![]() ∠BAC=60°,于是
∠BAC=60°,于是 ![]() =
= ![]() =
= ![]() ; 迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.
; 迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.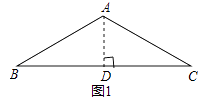
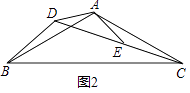
(1)①求证:△ADB≌△AEC;②请直接写出线段AD,BD,CD之间的等量关系式;
(2)拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF. 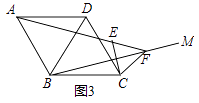
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
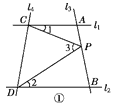
【题目】如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
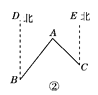
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
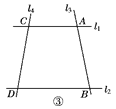
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC. 
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PCPA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形 ABCD中,O为 AC 的中点,过点O的直线分别与AB,CD交于点E,F,连接 BF交AC于点M连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①△AOE≌△COF;②△EOB≌△CMB;③FB⊥OC,OM=CM;④四边形 EBFD 是菱形;⑤MB:OE=3:2其中正确结论的个数是( )
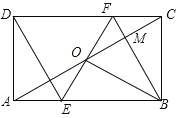
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从甲、乙两名同学中挑选一人参加创新能力大赛,在最近的五次选拔测试中, 他俩的成绩分别如下表,请根据表中数据解答下列问题:
第 1 次 | 第 2 次 | 第 3 次 | 第 4 次 | 第 5 次 | 平均分 | 众数 | 中位数 | 方差 | |
甲 | 60 分 | 75 分 | 100 分 | 90 分 | 75 分 | 80 分 | 75 分 | 75 分 | 190 |
乙 | 70 分 | 90 分 | 100 分 | 80 分 | 80 分 | 80 分 | 80 分 |
(1)把表格补充完整:
(2)在这五次测试中,成绩比较稳定的同学是多少;若将 80 分以上(含 80 分) 的成绩视为优秀,则甲、乙两名同学在这五次测试中的优秀率分别是多少;
(3)历届比赛表明,成绩达到80分以上(含 80分)就很可能获奖,成绩达到 90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九(1)、九(2)两班的班长交流了为四川安雅地震灾区捐款的情况:
(Ⅰ)九(1)班班长说:“我们班捐款总数为1200元,我们班人数比你们班多8人.”
(Ⅱ)九(2)班班长说:“我们班捐款总数也为1200元,我们班人均捐款比你们班人均捐款多20%.”
请根据两个班长的对话,求这两个班级每班的人均捐款数.
查看答案和解析>>
科目:初中数学 来源: 题型:
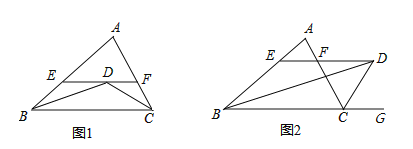
【题目】(1)如图1所示,在△ABC中,EF∥BC,点D在EF上,BD、CD分别平分∠ABC、∠ACB,若已知BE=3,CF=5,求EF的长度;
(2)如图2所示,BD平分∠ABC、CD平分∠ACG,DE∥BC交AB于点E,交AC于点F,线段EF与BE、CF有什么数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分) 如图1,将△ABC纸片沿中位线EH折叠,使点A的对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形.类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩 形,这样的矩形称为叠合矩形.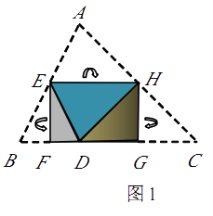
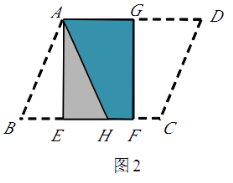

(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段 , ;S矩形AEFG:S□ABCD=
(2)ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长.
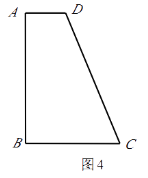
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10.小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出AD,BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com