
【题目】若﹣1是关于x的方程mx﹣n=1(m≠0)的解,则关于x的方程(m+n)(2x+1)﹣n﹣m=0(m≠n)的解为_____.
科目:初中数学 来源: 题型:
【题目】在一个木箱中装有卡片共50张,这些卡片共有三种,它们分别标有1、2、3的字样,除此之外都相同,其中标有数字2的卡片比标有数字3的卡片的3倍少8张,已知从木箱中随机摸出一张标有数字1的卡片的概率是![]() .
.
(1)求木箱中标有数字1的卡片的张数.
(2)求从木箱中随机摸出一张标有数字3的卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个一次函数的图象,甲、乙两位同学分别说出了它的一些特点:
甲:y随x的增大而减小; 乙:当x<0时,y>3.
请你写出满足甲、乙两位同学要求的一个一次函数表达式____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两角之比为2:1,且这两角之和为直角,则这两个角的大小分别为( )
A. 70°,22° B. 60°,30° C. 50°,40° D. 55°,35°
查看答案和解析>>
科目:初中数学 来源: 题型:
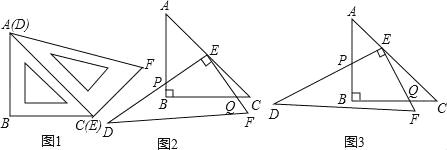
【题目】如图1,一副直角三角板满足AB=BC,AC=DE,∠ABC=∠DEF=90°,∠EDF=30°,
【操作1】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上,再将三角板DEF绕点E旋转,并使边DE与边AB交于点P,边EF与边BC于点Q.
在旋转过程中,如图2,当![]() 时,EP与EQ满足怎样的数量关系?并给出证明.
时,EP与EQ满足怎样的数量关系?并给出证明.
【操作2】在旋转过程中,如图3,当![]() 时EP与EQ满足怎样的数量关系?,并说明理由.
时EP与EQ满足怎样的数量关系?,并说明理由.
【总结操作】根据你以上的探究结果,试写出![]() 当时,EP与EQ满足的数量关系是什么?其中m的取值范围是什么?(直接写出结论,不必证明).
当时,EP与EQ满足的数量关系是什么?其中m的取值范围是什么?(直接写出结论,不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论. 
解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2= . ( . ),
∴AB∥EF( . )
∴∠3= . ( . )
又∠B=∠3(已知)
∴∠B= . (等量代换)
∴DE∥BC( . )
∴∠C=∠AED( . ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高速公路的同一侧有A、B两城镇,如图,它们到高速公路所在直线MN的距离分别为AA′=2 km,BB′=4 km,A′B′=8 km.要在高速公路上A′、B′之间建一个出口P,使A、B两城镇到P的距离之和最小.求这个最短距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com