
 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源:2017届辽宁省九年级3月月考数学试卷(解析版) 题型:单选题
某省为了实现到2017年全省森林覆盖率达到63%的目标,已知2015年全省森林覆盖率为60.05%,设从2015年起该省森林覆盖率的年平均增长率为x,则可列方程为 ( )
A. 60.05(1+2x)=63% B. 60.05(1+2x)=63
C. 60.05(1+x)2=63% D. 60.05(l+x)2=63
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15 | B. | 10 | C. | 8 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
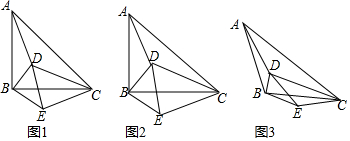
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
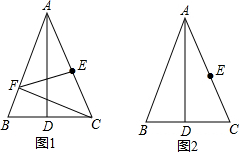
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
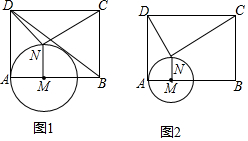
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
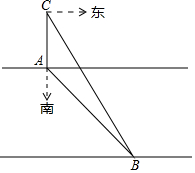 某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点A处,测得河的南岸边点B在其南偏东45°方向,然后向北走20米到达C点,测得点B在点C的南偏东33°方向,求出这段河的宽度(结果精确到1米,参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,$\sqrt{2}$≈1.41)
某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点A处,测得河的南岸边点B在其南偏东45°方向,然后向北走20米到达C点,测得点B在点C的南偏东33°方向,求出这段河的宽度(结果精确到1米,参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,$\sqrt{2}$≈1.41)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com