已知抛物线y=ax2+bx+c与y轴交于点C,与x轴交于点A(x1,0)、B(x2,0)(x1<x2),顶点M的纵坐标为-4,若x1、x2是方程x2-2(m-1)x+m2-7=0的两个根,且x21+x22=10.
(1)求A、B两点的坐标;
(2)求抛物线的解析式及点C的坐标;
(3)在抛物线上是否存在点P,使三角形PAB的面积等于四边形ACMB的面积的2倍?若存在,求出所有符合条件的点的坐标;若不存在,请说明理由.

解:(1)∵x
1,x
2是方程x
2-2(m-1)x+m
2-7=0的两个根,
∴x
1+x
2=2(m-1),x
1•x
2=m
2-7.
又∵x
12+x
22=10,
∴(x
1+x
2)
2-2x
1x
2=10,
∴[2(m-1)]
2-2(m
2-7)=10,
即m
2-4m+4=0.
解得:m
1=m
2=2.
将m=2代入方程x
2-2(m-1)x+m
2-7=0,
得:x
2-2x-3=0,
解得:x
1=-1,x
2=3.
∴点A的坐标为(-1,0),点B的坐标为(3,0).
(2)因为抛物线与x轴的交点为A(-1,0)、B(3,0),由对称性可知,顶点M的横坐标为1,则顶点M的坐标为(1,-4).
∴
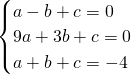
,
解得:

,
∴抛物线的解析式为y=x
2-2x-3.
在y=x
2-2x-3中,
令x=0,得y=-3.
∴点C的坐标为(0,-3).
(3)设抛物线的对称轴与x轴交于点D,
则AO=OD=1,DB=2,OC=3,
DM=4,AB=4.
∴S
四边形ACMB=S
△ACO+S
梯形OCMD+S
△DMB
=

•AO•CO+

(CO+MD)+

DB•MD
=

×1×3+

×(3+4)×1+

×2×4=9.
设P(x
0,y
0)为抛物线上一点,
则S
△PAB=

AB•|y
0|.
若S
△PAB=2S
四边形ACMB,
则

•AB•|y
0|=18,
∴丨y
0丨=9,y
0=±9.
将y
0=9代入y=x
2-2x-3中,得x
2-2x-3=9,
即x
2-2x-12=0,
解得:x
1=1-

,x
2=1+

.
将y
0=-9代入y=x
2-2x-3中,得:x
2-2x-3=-9,
即x
2-2x+6=0.
∵△=(-2)
2-4×1×6=-20<0,
∴此方程无实数根.
∴符合条件的点P有两个:P
1(1-

,9),P
2(1+

,9).
分析:(1)根据一元二次方程根与系数的关系,建立关于m的方程,然后解答即可求出m的值;
(2)根据A、B的横坐标,求出M的横坐标,从而得到M的坐标,然后利用待定系数法求出函数解析式,令x=0,即可得到y=-3,从而得到函数解析式.
(3)假设存在点P,根据S
四边形ACMB=S
△ACO+S
梯形OCMD+S
△DMB,求出四边形的面积,根据S
△PAB=2S
四边形ACMB,建立关于m的解析式,据此解答即可.
点评:本题考查了二次函数的综合题型,其中涉及到的知识点有抛物线的顶点求法和三角形的面积求法.在求存在性问题时,要假设该点存在,然后进行计算,若得出矛盾,则不存在,否则,存在.

 解:(1)∵x1,x2是方程x2-2(m-1)x+m2-7=0的两个根,
解:(1)∵x1,x2是方程x2-2(m-1)x+m2-7=0的两个根,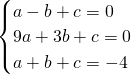 ,
, ,
, •AO•CO+
•AO•CO+ (CO+MD)+
(CO+MD)+ DB•MD
DB•MD ×1×3+
×1×3+ ×(3+4)×1+
×(3+4)×1+ ×2×4=9.
×2×4=9. AB•|y0|.
AB•|y0|. •AB•|y0|=18,
•AB•|y0|=18, ,x2=1+
,x2=1+ .
. ,9),P2(1+
,9),P2(1+ ,9).
,9).

 名校通行证有效作业系列答案
名校通行证有效作业系列答案 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=