练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知等边三角形ABC的高为4，在这个三角形所在的平面内有一点P，若点P到AB的距离是1，点P到AC的距离是2，则点P到BC的最小距离和最大距离分别是__________．


    1和7  点拨：点P可在三角形内和三角形外，需要分情况求解．设点P到△ABC三边AB、AC、BC（或其延长线）的距离分别为，△ABC的高为h．（1）当点P在等边三角形ABC内时：连接PA、PB、PC，利用面积公式可得，则，所以点P到BC的最小距离是1；（2）当点P在等边三角形ABC外时（只考虑P离BC最远时的情况）：同理可得，此时.综上可知，点P到BC的最小距离和最大距离分别是1和7.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    有些大数值问题可以通过用字母代替数，转化成整式问题来解决，请先阅读下面的解题过程，再解答后面的问题．

    例：若x＝123456789×123456786，y＝123456788×123456787，试比较x、y的大小．

    解：设123456788＝a，那么x＝(a＋1)(a－2)＝a2－a－2，y＝a(a－1)＝a2－a，

    ∵x－y＝(a2－a－2)－(a2－a)＝－2＜0，∴x＜y.

    看完后，你学到这种方法了吗？再亲自试一试吧，你准行！

    问题：计算1.35×0.35×2.7－1.353－1.35×0.352．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列数中，无理数有　　　　　个.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列运算 正确的是（   ）

    A．        B．a÷b×=a      

    C．          D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图3所示，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正△ABC和正△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下四个结论：①△ACD≌△BCE；②AD=BE；③∠AOB=60°；④△CPQ是等边三角形．其中正确的是（   ）

    A．①②③④                B．②③④           

    C．①③④                  D．①②③

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图9，△ABC中，∠A=40°，∠B=76°，CE平分∠ACB，CD⊥AB于D，DF⊥CE交CE于F，求∠CDF的度数．

     

    图9

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图12所示，已知△ABC中，AB＝AC＝10厘米，BC＝8厘米，点D为AB的中点．

     

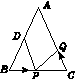
    图12

    （1）如果点P在线段BC上以1厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动．

    ①若点Q的运动速度与点P的运动速度相等，经过3秒后，△BPD与△CQP是否全等？请说明理由；

    ②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

     （2）若点Q以（1）②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    观察下列图形中点的个数，若按其规律再画下去，可以得到第n个图形中所有的个数为

                     （用含n的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若已知x＋y＝3，xy＝1，试分别求出 和的值．

    查看答案和解析>>

    同步练习册答案