某中学为打造“书香校园”,计划用不超过1900本科技类书籍和1610本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是700元,组建一个小型图书角的费用是500元,试说明哪种方案费用最低,最低费用是多少元?
解:(1)设组建中型图书角x个,则组建小型图书角为(30-x)个.
由题意,得
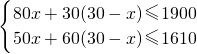
,
解这个不等式组,得
19x≤20.
由于x只能取整数,
∴x的取值是19,20.
当x=19时,30-x=11;
当x=20时,30-x=10.
故有2组建方案:
方案一,组建中型图书角19个,小型图书角11个;
方案二,组建中型图书角20个,小型图书角10个.
(2)方法一:假设总费用为w,
∴w=700x+500(30-x),
=200x+15000,
∵w随x的增大而增大,
∴当x取最小值19时,总费用最低,最低费用是200x+15000=200×19+15000=18800元.
∴组建中型图书角19个,小型图书角11个,总费用最低,最低费用是18800元.
分析:(1)设组建中型图书角x个,则组建小型图书角为(30-x)个.
根据不等关系:①科技类书籍不超过1900本;②人文类书籍不超过1610本.列不等式组,进行求解;
(2)首先得出W与x之间的函数的关系,再利用一次函数的增减性得出x的值.
点评:此题主要考查了一次函数的应用,解答本题的关键是正确找到题目中的不等关系,列不等式组求得方案的个数.

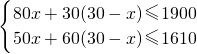 ,
,
