
 如图,小勇要用长20m的铁栏杆,一面靠墙AD,围成一个矩形的花圃(墙足够长).求AB的长为多少时,花圃的面积最大?并求出这个最大面积.
如图,小勇要用长20m的铁栏杆,一面靠墙AD,围成一个矩形的花圃(墙足够长).求AB的长为多少时,花圃的面积最大?并求出这个最大面积. 时取得.
时取得. 

科目:初中数学 来源: 题型:
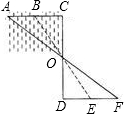 如图,小勇要测量家门前河中浅滩B到对岸A的距离,先在岸边定出C点,使C,A,B在同一直线上,再依AC的垂直方向在岸边画CD,取它的中点O,又画DF⊥CD,观测得到E,O,B在同一直线上,且F,O,A也在同一直线上,那么EF的长就是浅滩B和对岸A的距离,你能说出这是为什么吗?
如图,小勇要测量家门前河中浅滩B到对岸A的距离,先在岸边定出C点,使C,A,B在同一直线上,再依AC的垂直方向在岸边画CD,取它的中点O,又画DF⊥CD,观测得到E,O,B在同一直线上,且F,O,A也在同一直线上,那么EF的长就是浅滩B和对岸A的距离,你能说出这是为什么吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
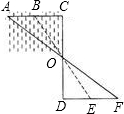 如图,小勇要测量家门前河中浅滩B到对岸A的距离,先在岸边定出C点,使C,A,B在同一直线上,再依AC的垂直方向在岸边画CD,取它的中点O,又画DF⊥CD,观测得到E,O,B在同一直线上,且F,O,A也在同一直线上,那么EF的长就是浅滩B和对岸A的距离,你能说出这是为什么吗?
如图,小勇要测量家门前河中浅滩B到对岸A的距离,先在岸边定出C点,使C,A,B在同一直线上,再依AC的垂直方向在岸边画CD,取它的中点O,又画DF⊥CD,观测得到E,O,B在同一直线上,且F,O,A也在同一直线上,那么EF的长就是浅滩B和对岸A的距离,你能说出这是为什么吗?查看答案和解析>>
科目:初中数学 来源:2006-2007学年北京市海淀区九年级(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com