
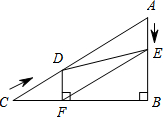
 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts(0<t≤15).过点DDF⊥BC于点F,连接DE,EF.
如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts(0<t≤15).过点DDF⊥BC于点F,连接DE,EF.分析 (1)根据时间和速度表示出AE和CD的长,利用30°所对的直角边等于斜边的一半求出DF的长为4t,则AE=DF,再证明,AE∥DF即可解决问题.
(2)①根据(1)的结论可以证明四边形AEFD为平行四边形,如果四边形AEFD能够成为菱形,则必有邻边相等,则AE=AD,列方程求出即可;
②由题意得出∠ADE=∠C=30°,由直角三角形的性质得出AD=2AE,得出方程,解方程即可.
解答 (1)证明:由题意得:AE=2t,CD=4t,
∵DF⊥BC
∴∠CFD=90°,
∵∠C=90°-60°=30°,
∴DF=$\frac{1}{2}$CD=$\frac{1}{2}$×4t=2t,
∴AE=DF;
∵DF⊥BC,
∴∠CFD=∠B=90°,
∴DF∥AE,
∴四边形AEFD是平行四边形.
(2)解:①∵DF⊥BC
∴∠CFD=90°
∵∠B=90°
∴∠B=∠CFD
∴DF∥AB,
由(1)得:DF=AE=2t,
∴四边形AEFD是平行四边形,
当AD=AE时,四边形AEFD是菱形,
即60-4t=2t,
解得:t=10,
即当t=10时,?AEFD是菱形,
故答案为:10;
②若四边形DEBF为矩形.则DE⊥AB,
∴DE∥BC,
∴∠ADE=∠C=30°
∴AD=2AE,
∵CD=4t,
∴DF=2t=AE,
∴AD=4t,
∴4t=60-4t,
∴t=7.5;
故答案为:7.5.
点评 本题是四边形综合题目,考查了直角三角形的性质、平行四边形的判定、菱形的性质、矩形的性质等知识点,熟练掌握平行四边形、菱形的判定是解题的关键.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{64}$=4 | B. | $\sqrt{16}$=±4 | C. | $\sqrt{-9}$=3 | D. | $\sqrt{2\frac{1}{4}}$=$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B. | $\sqrt{8}$÷$\sqrt{2}$=4 | C. | 5$\sqrt{3}$-$\sqrt{27}$=2$\sqrt{3}$ | D. | $\sqrt{{x}^{2}}$=x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠ACB=90°,AC=5cm,AB=13cm,将△ABC绕点B顺时针旋转60°,得到△EBD,连接DC,则△BCD的周长为36cm.
如图,在Rt△ABC中,∠ACB=90°,AC=5cm,AB=13cm,将△ABC绕点B顺时针旋转60°,得到△EBD,连接DC,则△BCD的周长为36cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
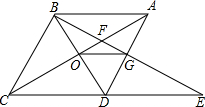 如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE,分别交AC,AD于点F、G,连结OG,则下列结论:
如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE,分别交AC,AD于点F、G,连结OG,则下列结论:| A. | ①③ | B. | ①③④ | C. | ①②③ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
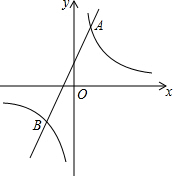 已知反比例函数y=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
已知反比例函数y=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com