
在△ABC中, BE=BF,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30º,求∠ACF度数.( 根据2011重庆江津第22题改编)
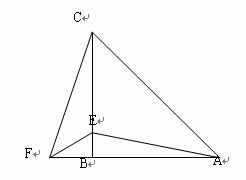
解:(1)∵∠ABC=90°,∴∠CBF=∠ABE=90°. …………………………1分
在Rt△ABE和Rt△CBF中,
∵AE=CF,![]() BE=BF, ……………………………………………………2分
BE=BF, ……………………………………………………2分
∴Rt△ABE≌Rt△CBF(HL) ……………………………………………………1分
(2)∵AB=BC, ∠ABC=90°, ∴ ∠CAB=∠ACB=45°. …………………………1分
∵∠BAE=∠CAB-∠CAE=45°-30°=15°. …………………………1分
由(1)知 Rt△ABE≌Rt△CBF, ∴∠BCF=∠BAE=15°, …………………………1分
∴∠ACF=∠BCF+∠ACB=45°+15°=60°…………………………1分


科目:初中数学 来源: 题型:
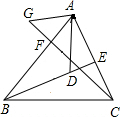 已知:如图,在△ABC中,BE、CF分别是AC、AB两条边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连AD、AG.求证:AG=AD.
已知:如图,在△ABC中,BE、CF分别是AC、AB两条边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连AD、AG.求证:AG=AD.查看答案和解析>>
科目:初中数学 来源: 题型:
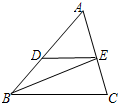 (2013•徐汇区一模)如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(2013•徐汇区一模)如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,BE、CF分别是∠ABC和∠ACB的角平分线,并相交于点D,EG,FG分别是∠AEB和∠AFC的角平分线,并相交于点G,如果∠A=40°,那么∠CDB=
如图,在△ABC中,BE、CF分别是∠ABC和∠ACB的角平分线,并相交于点D,EG,FG分别是∠AEB和∠AFC的角平分线,并相交于点G,如果∠A=40°,那么∠CDB=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com