
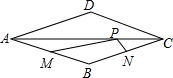
 菱形ABCD的两条对角线的长分别为6和8,点M、N分别是边AB、BC的中点,点P是对角线AC上的一个动A点,则PM+PN的最小值是________.
菱形ABCD的两条对角线的长分别为6和8,点M、N分别是边AB、BC的中点,点P是对角线AC上的一个动A点,则PM+PN的最小值是________. 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:学习周报 数学 华师大八年级版 2009-2010学年 第18期 总第174期 华师大版 题型:013
如图,已知AC、BD是菱形ABCD的两条对角线,且相交于点O,则下面说法正确的是

图中共有五个三角形,它们不全等
图中有五个全等的直角三角形
图中有四对全等的直角三角形
图中有四个全等的直角三角形,两对全等的等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
查看答案和解析>>
科目:初中数学 来源:期末题 题型:填空题
 )。
)。 )。
)。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com