
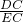 =2,
=2,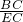 =4,
=4, =2,
=2,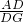 =4,
=4,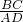 =
=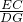 ,
, =
=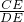 ,
,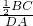 =
= ,
,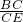 =
=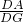 ,∠ADE=∠C,
,∠ADE=∠C,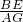 =
=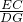 =4,
=4, =
= =2,
=2, ,
, a,则GE=
a,则GE= a,EC=4
a,EC=4 a,DC=10a,
a,DC=10a, a,
a,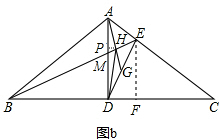
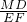 =
=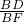 ,
,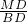 =
= =
=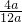 =
= =tan∠MBD=tan∠DAG=
=tan∠MBD=tan∠DAG= ,
,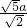 =
= a,
a, a=1,
a=1, ,AD=3,
,AD=3, ,AP=
,AP= ,DP=
,DP= ,PH=
,PH= ,
,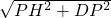 =
= .
.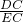 =2,所以
=2,所以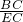 =4,同理可得在Rt△ADE中,
=4,同理可得在Rt△ADE中, =2,
=2,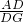 =4,
=4,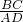 =
=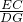 ,再由∠ADE=∠C即可得出结论;
,再由∠ADE=∠C即可得出结论; =
=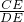 ,即
,即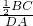 =
= ,
,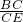 =
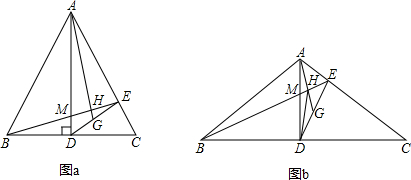
=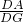 ,∠ADE=∠C,进而得出△ADG∽△BCE,tanC=
,∠ADE=∠C,进而得出△ADG∽△BCE,tanC= ,故可得出∠AHE=∠ADB=90°,设DG=
,故可得出∠AHE=∠ADB=90°,设DG= a,则GE=
a,则GE= a,EC=4
a,EC=4 a,DC=10a,所以AD=5a,AE=
a,DC=10a,所以AD=5a,AE= a,∠AGE=45°,过点E作EF⊥BC于点F,过点H作GP⊥AD于点P,根据MD∥EF可知△BMD∽△BEF,所以
a,∠AGE=45°,过点E作EF⊥BC于点F,过点H作GP⊥AD于点P,根据MD∥EF可知△BMD∽△BEF,所以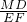 =
=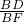 ,
,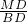 =
= =
=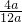 =
= =tan∠MBD=tan∠DAG=
=tan∠MBD=tan∠DAG= ,在Rt△AHE中可用a表示出AH的长,在Rt△AMH中,根据AM=
,在Rt△AHE中可用a表示出AH的长,在Rt△AMH中,根据AM= a=1求出a的值,故可得出AH,AP,DP,PH的长,根据勾股定理即可得出结论.
a=1求出a的值,故可得出AH,AP,DP,PH的长,根据勾股定理即可得出结论.

 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
 如图,在△ABC中,AB=AC,∠A=36°,
如图,在△ABC中,AB=AC,∠A=36°,| CD | DA |
查看答案和解析>>
科目:初中数学 来源: 题型:
 ,连接AO、BE、DC.
,连接AO、BE、DC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com