探究:证明:∵根据旋转的性质得:△EBC≌△FDC,
∴CE=CF,DF=BE,
∵CG平分∠ECF,
∴∠ECG=∠FCG,
在△ECG和△FCG中

∴△ECG≌△FCG(SAS),
∴EG=GF,
∵GF=DG+DF=DG+BE,
∴EG=BE+GD;

应用:
解:如图3,过C作CH⊥AD于H,旋转△BCE到△CHM,
则∠A=∠B=∠CHA=90°,
∵AB=BC,
∴四边形ABCH是正方形,
∵∠DCE=45°,AH=BC,
∴∠DCH+∠ECB=90°-45°=45°,
∵由已知证明知:△EBC≌△MHC,
∴∠ECB=∠MCH,
∴∠DCH+∠MCH=45°,
∴CD平分∠ECM,
∴由探究证明知:DE=BE+DH,
在Rt△AED中,DE=10,AD=6,由勾股定理得:AE=8,
设BE=x,则BC=AB=x+8=AH,
即x+8=6+10-x,
x=4,
BE=4,
AB=4+8=12,BC=AB=12,
∴梯形ABCD的面积是

×(6+12)×12=108.
分析:探究:求出CE=CF,DF=BE,∠ECG=∠FCG,证△ECG≌△FCG,推出EG=GF即可;
应用:过C作CH⊥AD于H,旋转△BCE到△CHM,推出四边形ABCH是正方形,CD平分∠ECM,由探究证明知:DE=BE+DH,
在Rt△AED中,DE=10,AD=6,由勾股定理求出AE=8,设BE=x,根据BC=AB=x+8=AH得出x+8=6+10-x,求出x=4即可.
点评:本题考查了正方形性质,全等三角形的性质和判定,三角形的内角和定理的应用,主要考查学生综合运用性质进行推理的能力.




 ×(6+12)×12=108.
×(6+12)×12=108.

 阅读快车系列答案
阅读快车系列答案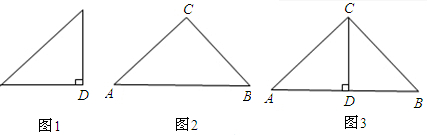

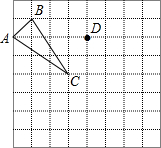 如图,△ABC在正方形网格中(每个小方格都是边长为1的正方形),请解答下列问题:
如图,△ABC在正方形网格中(每个小方格都是边长为1的正方形),请解答下列问题: