
如图,在⊙O中,∠ACB=∠BDC=60°,AC=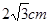 ,
,
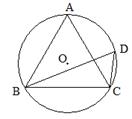
(1)判断△ABC的形状并证明你的结论;
(2)求⊙O的周长
(1)见解析(1)4π
【解析】
试题分析:利用圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状(2)由三角形内角和得∠ABC=60°,所以△ABC是等边三角形,作OE⊥AC,连接OA,由垂径定理得,AE=CE=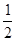 AC=
AC=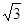 cm,再由余弦的概念求得半径OA的长,由圆的周长公式求得周长.
cm,再由余弦的概念求得半径OA的长,由圆的周长公式求得周长.
解:(1)△ABC为等边三角形证明如下:
∵∠BAC和∠BDC都是弧BC所对的圆周角
∴∠BAC=∠BDC
∵∠ACB=∠BDC=60° ∴∠BAC =∠ACB =60°
∴△ABC为等边三角形……………………3分
(2)过O点作OE⊥AC于E点,连接OA
∵AC=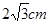 ∴AE=CE=
∴AE=CE=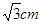
∵△ABC为等边三角形
∴∠OAE=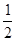 ∠BAC=30° 设OE=x,则OA=2x,
∠BAC=30° 设OE=x,则OA=2x,
在Rt△OAE中,有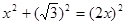 ,解之得x=1
,解之得x=1
∴OA=2 即⊙O的周长=2×2×π=4πcm
考点:圆周角定理;圆心角、弧、弦的关系;等边三角形的性质;圆的认识;解直角三角形.
点评:本题考查了圆周角定理.同弧所对的圆周角相等,并且等于它所对的圆心角的一半.也考查了等边三角形的判定方法.本题利用了圆周角定理,等边三角形的判定和性质,垂径定理,余弦的概念,圆周长公式求解.


科目:初中数学 来源: 题型:
 19、如图,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,试说明∠1=∠2,以下是证明过程,请填空:
19、如图,在△ABC中,CD⊥AB于D,FG⊥AB于G,ED∥BC,试说明∠1=∠2,以下是证明过程,请填空:查看答案和解析>>
科目:初中数学 来源: 题型:
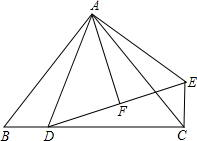 如图,在△ABC中,已知AB=AC,∠BAC=90°,D是BC上一点,EC⊥BC,EC=BD,DF=FE.求证:
如图,在△ABC中,已知AB=AC,∠BAC=90°,D是BC上一点,EC⊥BC,EC=BD,DF=FE.求证:查看答案和解析>>
科目:初中数学 来源: 题型:
 15、如图,在△ABC中,AQ=PQ,PR=PS,PS⊥AC于S,PR⊥AB于R,则以下结论中:(1)AS=AR;(2)△BRP∽△QSP;(3)PQ∥AB中,正确的有
15、如图,在△ABC中,AQ=PQ,PR=PS,PS⊥AC于S,PR⊥AB于R,则以下结论中:(1)AS=AR;(2)△BRP∽△QSP;(3)PQ∥AB中,正确的有查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com