解:∵∠C=90°,AC=6,BC=8,
∴AB=

=

=10,
∵S
△PBC=S
△ABC,
∴点P到BC的距离等于AC的长度,为6,
①如图1,点A、P在BC的同侧时,∵点A、P到BC的距离相等,
∴PA∥BC,
∴∠PAD=∠ABC,
过点P作PD⊥AB于点D,
∵PA=PB,
∴AD=

AB=

×10=5,
∵cos∠PAD=

=

,cos∠ABC=

=

=

,
∴

=

,
解得PA=

;
②如图2,点A、P在BC异侧时,过点P作PD⊥AB于D,

∵PA=PB,
∴AD=

AB=

×10=5,
过点D作DE∥BC,过点P作PE⊥BC相交于点E,
∵点D是AB的中点,
∴点E到BC的距离为

AC=

×6=3,
∴PE=3+6=9,
∵∠BAC+∠ADE=90°,∠ADE+∠PDE=90°,
∴∠PDE=∠BAC,
∵cos∠PDE=
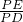
=

,cos∠BAC=

=

=

,
∴

=

,
解得PD=

,
在Rt△APD中,PA=
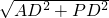
=

=

,
综上所述,PA的长为

或

.
分析:利用勾股定理列式求出AB的长度,根据等底等高的三角形面积相等可得点P到BC的距离等于点A到BC的距离相等,然后分①点A、P在BC的同侧时,PA∥BC,过点P作PD⊥AB于点D,根据等腰三角形三线合一的性质可得点D是AB的中点,然后求出AD的长,再利用∠PAD的余弦值列式求解即可;②点A、P在BC异侧时,过点P作PD⊥AB于D,根据等腰三角形三线合一的性质可得点D是AB的中点,过点D作DE∥BC,过点P作PE⊥BC相交于点E,先求出PE的长度,再根据同角的余角相等求出∠PDE=∠BAC,然后利用∠PDE的余弦值列式求解即可得到PD,在Rt△APD中,利用勾股定理列式进行计算即可得解.
点评:本题考查了等腰三角形三线合一的性质,三角形的面积勾股定理,锐角三角函数,根据等底等高的三角形的面积相等得到点A、P到BC的距离相等是解题的关键,要注意分两种情况讨论求解.

 Rt△ABC中,∠C=90°,AC=6,BC=8,P为△ABC所在平面上一点,PA=PB,且S△PBC=S△ABC,求PA的长.
Rt△ABC中,∠C=90°,AC=6,BC=8,P为△ABC所在平面上一点,PA=PB,且S△PBC=S△ABC,求PA的长. =
= =10,
=10, AB=
AB= ×10=5,
×10=5, =
= ,cos∠ABC=
,cos∠ABC= =
= =
= ,
, =
= ,
, ;
;
 AB=
AB= ×10=5,
×10=5, AC=
AC= ×6=3,
×6=3,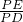 =
= ,cos∠BAC=
,cos∠BAC= =
= =
= ,
, =
= ,
, ,
,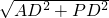 =
= =
= ,
, 或
或 .
.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案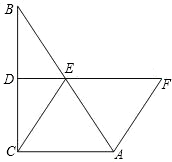 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形.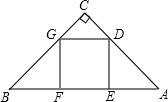 点G在边BC上.
点G在边BC上.