
分析 通过解一元一次方程组求得2<x<4.然后利用直接开平方法求得方程x2-12=0的根,由x的取值范围来取舍该方程的根.
解答 解:由$\left\{\begin{array}{l}{x+1<3x-3}\\{\frac{1}{2}(x-4)<\frac{1}{3}(x-4)}\end{array}\right.$求得$\left\{\begin{array}{l}{2<x}\\{x<4}\end{array}\right.$,
则2<x<4.
解方程x2-12=0可得x1=2$\sqrt{3}$,x2=-2$\sqrt{3}$,
∵2<2$\sqrt{3}$<4,符合题意
∴x=2$\sqrt{3}$.
点评 本题考查了解一元二次方程--公式法,解一元一次不等式组.要会熟练运用公式法求得一元二次方程的解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
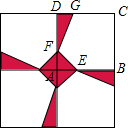 一个边长为8m的正方形花坛由4块全等的小正方形组成,在小正方形ABCD中,点G、E、F分别在CD、AB、AD上,且DG=1m,AE=AF,在△AEF、△DFG、五边形EBCGF三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元,问点E在什么位置时,正方形花坛种植花卉所需的总费用是715元?
一个边长为8m的正方形花坛由4块全等的小正方形组成,在小正方形ABCD中,点G、E、F分别在CD、AB、AD上,且DG=1m,AE=AF,在△AEF、△DFG、五边形EBCGF三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元,问点E在什么位置时,正方形花坛种植花卉所需的总费用是715元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每公顷所需生产组/个 | 每公顷雨季产值 | |
| 蔬菜 | $\frac{1}{2}$ | 52500 |
| 水稻 | $\frac{1}{4}$ | 18000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
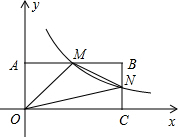 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,反比例函数y=$\frac{k}{x}$的图象经过点M,N,若M是AB的中点,△OMN的面积为3.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,反比例函数y=$\frac{k}{x}$的图象经过点M,N,若M是AB的中点,△OMN的面积为3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
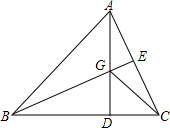 如图,在△ABC中,点D,E分别在BC,AC边上,E为AC的中点,AD,BE交于点G,BD=2DC,S△GEC=2,S△GDC=4,则△ABC的面积是( )
如图,在△ABC中,点D,E分别在BC,AC边上,E为AC的中点,AD,BE交于点G,BD=2DC,S△GEC=2,S△GDC=4,则△ABC的面积是( )| A. | 24 | B. | 30 | C. | 35 | D. | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
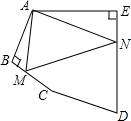 如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在BC,DE上分别找出一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为多少?
如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在BC,DE上分别找出一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com