
 如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB,BC延长线于F,E,求证:
如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB,BC延长线于F,E,求证:分析 (1)由AD的垂直平分线分别交AB、BC延长线于F、E,根据线段垂直平分线的性质,易得AE=DE,又由等边对等角的性质,证得∠EAD=∠EDA;
(2)由AD的垂直平分线分别交AB、BC延长线于F、E,可得AF=DF,又由AD是∠BAC平分线,易得∠FDA=∠CAD,即可判定DF∥AC;
(3)由三角形外角的性质,可得∠EAC=∠EAD-∠CAD,∠B=∠EDA-∠BAD,又由∠BAD=∠CAD,∠EAD=∠EDA,即可证得结论.
解答 证明:(1)∵EF是AD的垂直平分线,
∴AE=DE,
∴∠EAD=∠EDA;
(2)∵EF是AD的垂直平分线,
∴AF=DF,
∴∠FAD=∠FDA,
∵AD是∠BAC平分线,
∴∠FAD=∠CAD,
∴∠FDA=∠CAD,
∴DF∥AC;
(3)∵∠EAC=∠EAD-∠CAD,∠B=∠EDA-∠BAD,且∠BAD=∠CAD,∠EAD=∠EDA,
∴∠EAC=∠B.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
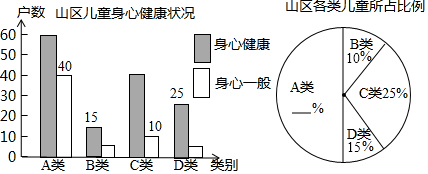
| 类别 | 现状 | 户数 | 比例 |
| A类 | 父母长年在外打工,孩子留在老家由老人照顾 | 100 | |
| B类 | 父母长年在外打工,孩子带在身边 | 10% | |
| C类 | 父母就近在城镇打工,晚上回家照顾孩子 | 50 | |
| D类 | 父母在家务农,并照顾孩子 | 15% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
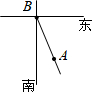 如图,如果张江高科技园区(A)位于复旦大学(B)的南偏东30°的方向,那么复旦大学(B)位于张江高科技园区(A)的北偏西30°或西偏北60°方向.
如图,如果张江高科技园区(A)位于复旦大学(B)的南偏东30°的方向,那么复旦大学(B)位于张江高科技园区(A)的北偏西30°或西偏北60°方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
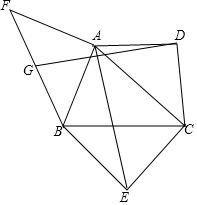 如图所示,已知△ABC是锐角三角形,以边AC、BC为斜边向形外作等腰直角三角形ACD和等腰直角三角形BCE,以边AB为直角边向形外作等腰直角三角形ABF,∠BAF=90°,点G为BF的中点,连接GD和AE,试探究GD和AE的数量关系和位置关系,并对你的结论加以证明.
如图所示,已知△ABC是锐角三角形,以边AC、BC为斜边向形外作等腰直角三角形ACD和等腰直角三角形BCE,以边AB为直角边向形外作等腰直角三角形ABF,∠BAF=90°,点G为BF的中点,连接GD和AE,试探究GD和AE的数量关系和位置关系,并对你的结论加以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com