练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    当x＝1，y＝-1时代数式ax+by-3的值为0，那么当x＝-1，y＝1时代数式ax+by-3的值为________.

    －6
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：非常讲解·教材全解全析数学八年级上(配课标北师大版) 课标北师大版 题型：022

    在代数式ax＋by中，当x＝2，y＝－3时，其值为5；当x＝－1，y＝2时，其值为．则当x＝1，y＝6时，代数式ax＋by的值为________．

    查看答案和解析>>

    科目：初中数学 来源：初中数学　三点一测丛书　八年级数学　下　（江苏版课标本） 江苏版 题型：044

    函数的奇偶性

    　　一般地，如果函数y＝f(x)对于自变量取值范围内的任意x，都有f(－x)＝－f(x)f那么y＝f(x)就叫做奇函数；如果函数y＝f(x)对于自变量取值范围内的任意x，都有f(－x)＝f(x)，那么y＝f(x)就叫做偶函数．

    　　例如：f(x)＝x3＋x．

    　　当x取任意实数，

    　　f(－x)＝(－x)3＋(－x)＝－x3－x＝－(x3＋x)

    　　即f(－x)＝－f(x)

    　　所以f(x)＝x3＋x为奇函数．

    　　又如：f(x)＝|x|，

    　　当x取任意实数时，f(－x)＝|－x|＝|x|＝f(x)，

    　　即f(－x)＝f(x)

    　　所以f(x)为偶函数．

    问题：(1)下列函数：

    ①y＝x4；②y＝x2＋1；③y＝；④y＝；⑤y＝x＋．

    所有奇函数是________，所有偶函数是________(只填序号)；

    (2)请你再分别写出一个奇函数，一个偶函数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    数学课堂上，徐老师出示一道试题：如图（十）所示，在正三角形ABC中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠ACP的平分线上一点．若∠AMN＝60°，求证：AM＝MN．
        
    (1)经过思考，小明展示了一种正确的证明过程．请你将证明过程补充完整．
    证明：在AB上截取EA＝MC，连结EM，得△AEM．
    ∵∠1＝180°－∠AMB－∠AMN，∠2＝180°－∠AMB－∠B，∠AMN＝∠B＝60°，∴∠1＝∠2．
    又CN平分∠ACP，∠4＝∠ACP＝60°．∴∠MCN＝∠3＋∠4＝120°…………①
    又∵BA＝BC，EA＝MC，∴BA－EA＝BC－MC，即BE＝BM．
    ∴△BEM为等边三角形．∴∠6＝60°．
    ∴∠5＝180°－∠6＝120°．………②
    ∴由①②得∠MCN＝∠5．
    在△AEM和△MCN中，
    ∵________________________________
    ∴△AEM≌△MCN (ASA)．∴AM＝MN．
    (2)若将试题中的“正三角形ABC”改为“正方形A1B1C1D1”（如图），N1是∠D1C1P1的平分线上一点，则当∠A1M1N1＝90°时，结论A1M1＝M1N1．是否还成立？（直接写出答案，不需要证明）
    (3)若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”，请你猜想：当∠AnMnNn＝   °时，结论AnMn＝MnNn仍然成立？（直接写出答案，不需要证明）

    查看答案和解析>>

    科目：初中数学 来源：湖北省鄂州市2011年中考数学试题 题型：解答题

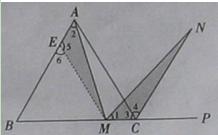
    数学课堂上，徐老师出示一道试题：

        如图（十）所示，在正三角形ABC中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠ACP的平分线上一点．若∠AMN＝60°，求证：AM＝MN．

    (1)经过思考，小明展示了一种正确的证明过程．请你将证明过程补充完整．

        证明：在AB上截取EA＝MC，连结EM，得△AEM．

        ∵∠1＝180°－∠AMB－∠AMN，∠2＝180°－∠AMB－∠B，∠AMN＝∠B＝60°，∴∠1＝∠2．

        又CN平分∠ACP，∠4＝∠ACP＝60°．∴∠MCN＝∠3＋∠4＝120°…………①

    又∵BA＝BC，EA＝MC，∴BA－EA＝BC－MC，即BE＝BM．

    ∴△BEM为等边三角形．∴∠6＝60°．

    ∴∠5＝180°－∠6＝120°．………②

    ∴由①②得∠MCN＝∠5．

    在△AEM和△MCN中，

    ∵                                            

    ∴△AEM≌△MCN (ASA)．∴AM＝MN．

    (2)若将试题中的“正三角形ABC”改为“正方形A1B1C1D1”（如图），N1是∠D1C1P1的平分线上一点，则当∠A1M1N1＝90°时，结论A1M1＝M1N1．是否还成立？（直接写出答案，不需要证明）

    (3) 若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”，请你猜想：当∠AnMnNn＝    °时，结论AnMn＝MnNn仍然成立？（直接写出答案，不需要证明）

        

     

     

    查看答案和解析>>

    科目：初中数学 来源：2011年初中毕业升学考试（广东河源卷）数学 题型：解答题

    如图，D是△ABC的边BC的中点,过AD延长线上的点E作AD的垂线EF，E为垂足，EF与AB的延长线相交于点F，点O在AD上，AO＝CO，BC∥EF．

    (1)证明：AB＝AC；

    (2)证明：点O是△ABC的外接圆的圆心；

    (3)当AB＝5，BC＝6时，连接BE，若∠ABE＝90°，求AE的长．

     

    查看答案和解析>>

    同步练习册答案