AD是△ABC的高,延长AD至E,使DE=AD,连接BE,CE.
(1)画出图形;
(2)指出图中一对全等三角形,并给出证明.
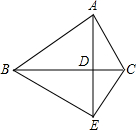
解:如图,
有△ABD≌△EBD,△ACD≌△ECD.
证明如下:
DE=AD,AD⊥BC,
∴BC是AE的中垂线,
∴AB=BE,AC=CE
∵AB=BE,AD=DE,BD=BD,
∴△ABD≌△EBD,
∵AD=DE,BD=BD,AC=CE
∴△ACD≌△ECD.
分析:由于DE=AD,AD⊥BC,所以BC是AE的中垂线,由中垂线的性质知,AB=BE,AC=CE,故可由SSS证得△ABD≌△EBD,△ACD≌△ECD.
点评:本题利用了中垂线的判定和性质,全等三角形的判定求解.中垂线可以带来线段相等,也有角相等.
