
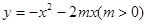 与
与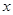 轴的另一个交点为A.过点
轴的另一个交点为A.过点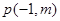 作直线
作直线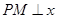 轴于点M,交抛物线于点B,过点B作直线BC∥
轴于点M,交抛物线于点B,过点B作直线BC∥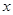 轴与抛物线交于点C(B、C不重合),连结CP.
轴与抛物线交于点C(B、C不重合),连结CP.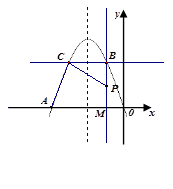
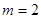 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;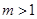 时,连结CA,问
时,连结CA,问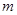 为何值时
为何值时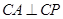 ?
?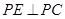 且
且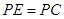 ,问是否存在
,问是否存在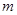 ,使得点E落在坐标轴上?若存在,求出所有满足要求的
,使得点E落在坐标轴上?若存在,求出所有满足要求的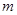 的值,并求出相对应的点E坐标;若不存在,请说明理由.
的值,并求出相对应的点E坐标;若不存在,请说明理由.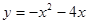 ,
,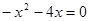 ,∴
,∴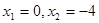
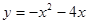 的对称轴为直线x=-2,
的对称轴为直线x=-2,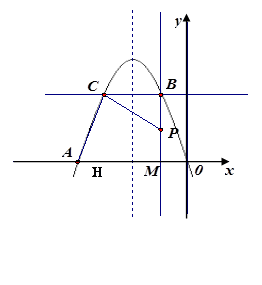
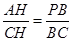 .
.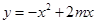 的对称轴为直线x=-m,其中m>1,
的对称轴为直线x=-m,其中m>1, ,
,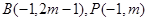
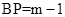

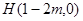 ,
,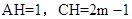
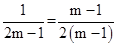 ∴
∴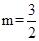 .
.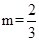 ,此时点E的坐标是
,此时点E的坐标是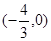 .
.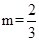 时,点E的坐标是
时,点E的坐标是 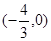 .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
 ,
, 分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有
分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有 ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线 交于点D,如图所示。
交于点D,如图所示。
 绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值; 绕点C旋转时,它与抛物线的另一个交点为P,请找出使△PCD为等腰三角形的点P,并求出点P的坐标。
绕点C旋转时,它与抛物线的另一个交点为P,请找出使△PCD为等腰三角形的点P,并求出点P的坐标。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
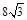 米.请你建立适当的平面直角坐标系解决下列问题.
米.请你建立适当的平面直角坐标系解决下列问题. 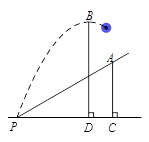
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
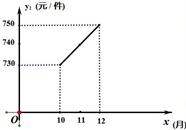
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.二次函数图像的对称轴是直线x=1; |
| B.当x>0时,y<4; |
| C.当x≤1时,函数值y是随着x的增大而增大; |
| D.当y≥0时,x的取值范围是-1≤x≤3时. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com