
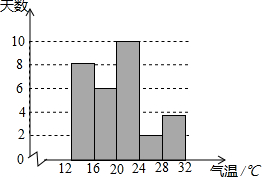
 为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.
为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.分析 (1)根据30天的最高气温总和除以总天数,即可得到这30天最高气温的平均数,再根据第15和16个数据的位置,判断中位数;
(2)根据30天中,最高气温超过(1)中平均数的天数,即可估计这个季度中最高气温超过(1)中平均数的天数;
(3)从6天中任选2天,共有15种等可能的结果,其中两天都在气温最高一组内的情况有6种,据此可得这两天都在气温最高一组内的概率.
解答 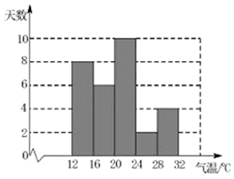 解:(1)这30天最高气温的平均数为:$\frac{14×8+18×6+22×10+26×2+30×4}{30}$=20.4℃;
解:(1)这30天最高气温的平均数为:$\frac{14×8+18×6+22×10+26×2+30×4}{30}$=20.4℃;
∵中位数落在第三组内,
∴中位数为22℃;
(2)∵30天中,最高气温超过(1)中平均数的天数为16天,
∴该地这个季度中最高气温超过(1)中平均数的天数为$\frac{16}{30}$×90=48(天);
(3)从6天中任选2天,共有15种等可能的结果,其中两天都在气温最高一组内的情况有6种,
故这两天都在气温最高一组内的概率为$\frac{6}{15}$=$\frac{2}{5}$.
点评 本题主要考查了频数分布直方图,平均数以及中位数的计算,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.解题时注意:如果一组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
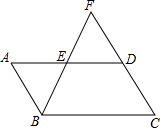 如图,?ABCD中,E为AD的中点,BE、CD相交于点F.
如图,?ABCD中,E为AD的中点,BE、CD相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
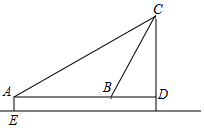 衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)
衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
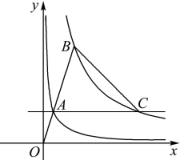 如图,分别位于反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$在第一象限图象上的两点A、B,与原点O在同一直线上,且$\frac{OA}{OB}$=$\frac{1}{3}$.
如图,分别位于反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$在第一象限图象上的两点A、B,与原点O在同一直线上,且$\frac{OA}{OB}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
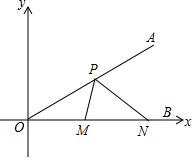 如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(3,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(3,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
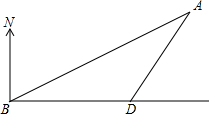 如图,海中有一小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?
如图,海中有一小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com