
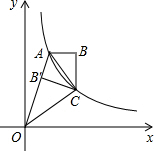
 如图,双曲线y=
如图,双曲线y=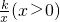 经过四边形OABC的顶点A、C,∠B=90°,OC平分OA与x轴的夹角,AB∥x轴,且S四边形OABC=2,将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则k=________.
经过四边形OABC的顶点A、C,∠B=90°,OC平分OA与x轴的夹角,AB∥x轴,且S四边形OABC=2,将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则k=________. k,则S△OCB′=
k,则S△OCB′= k,由AB∥x轴,得点A(x-a,2y),由题意得2y(x-a)=k,从而得出三角形ABC的面积等于
k,由AB∥x轴,得点A(x-a,2y),由题意得2y(x-a)=k,从而得出三角形ABC的面积等于 k,根据S四边形OABC=2,即可得出答案.
k,根据S四边形OABC=2,即可得出答案.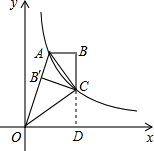
 (x>0)经过四边形OABC的顶点A、C,
(x>0)经过四边形OABC的顶点A、C, k,
k, k,
k, k,
k, k,
k, ay=
ay= k,
k, k+
k+ k+
k+ k=2,
k=2, k.
k. 

科目:初中数学 来源: 题型:
如图,双曲线![]() 经过四边形OABC的顶点 A、C,∠ABC= 900,OC平分OA与x轴正半轴的夹角. AB//x轴,将∆ABC沿AC翻折后得△AB’C,点B’落在 OA上,则四边形OABC的面积是______
经过四边形OABC的顶点 A、C,∠ABC= 900,OC平分OA与x轴正半轴的夹角. AB//x轴,将∆ABC沿AC翻折后得△AB’C,点B’落在 OA上,则四边形OABC的面积是______
查看答案和解析>>
科目:初中数学 来源:2012-2013学年湖北省鄂州市第三中学八年级下学期期中考试数学试卷(带解析) 题型:单选题
如图,双曲线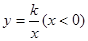 经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,若点A的坐标为(-6,4),则△AOC的面积为
经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,若点A的坐标为(-6,4),则△AOC的面积为
| A.12 | B.6 | C.9 | D.4 |
查看答案和解析>>
科目:初中数学 来源:2013届浙江省杭州市亭趾实验学校九年级上期中考试数学试卷(带解析) 题型:填空题
如图,双曲线 经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与
经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与 轴正半轴的夹角,AB∥
轴正半轴的夹角,AB∥ 轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是 _________.
轴,将△ABC沿AC翻折后得到△AB'C,B'点落在OA上,则四边形OABC的面积是 _________.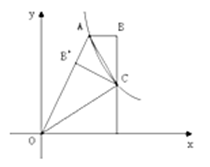
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江苏扬州卷)数学(解析版) 题型:填空题
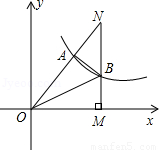
如图,双曲线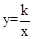 经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为5,则k的值是 ▲ .
经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为5,则k的值是 ▲ .
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省无锡市新区九年级下学期期中考试数学卷(解析版) 题型:填空题
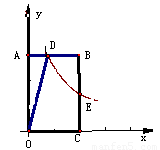
如图,双曲线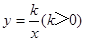 经过矩形QABC的边BC的中点E,交AB于点D。若梯形ODBC的面积为3,则双曲线的解析式为 ▲ .
经过矩形QABC的边BC的中点E,交AB于点D。若梯形ODBC的面积为3,则双曲线的解析式为 ▲ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com