
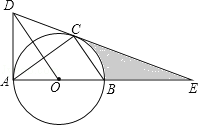
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AE=6,CE=2![]() ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
【答案】(1)、证明过程见解析;(2)、![]() .
.
【解析】
试题分析:(1)、连结OC,根据切线得出∠BAD=90°,然后得出△OCD和△OAD全等,从而得出∠OCD=∠OAD=90°,得出切线;(2)、设半径为r,则OE=AE﹣OA=6﹣r,OC=r,根据Rt△OCE的勾股定理求出r的值,然后根据△COE的面积减去扇形BOC的面积得出答案.
试题解析:(1)、连结OC,如图, ∵AD为⊙O的切线,∴AD⊥AB,∴∠BAD=90°,
∵OD∥BC,∴∠1=∠3,∠2=∠4, ∵OB=OC,∴∠3=∠4,∴∠1=∠2,
在△OCD和△OAD中,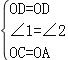 ,∴△AOD≌△COD(SAS); ∴∠OCD=∠OAD=90°,
,∴△AOD≌△COD(SAS); ∴∠OCD=∠OAD=90°,
∴OC⊥DE,∴DE是⊙O的切线;
(2)、设半径为r,则OE=AE﹣OA=6﹣r,OC=r,在Rt△OCE中,∵OC2+CE2=OE2,
∴r2+(2![]() )2=(6﹣r)2,解得r=2,∵tan∠COE=
)2=(6﹣r)2,解得r=2,∵tan∠COE=![]() =
=![]() =
=![]() ,∴∠COE=60°,
,∴∠COE=60°,
∴S阴影部分=S△COE﹣S扇形BOC=![]() ×2×2
×2×2![]() ﹣
﹣![]() =2
=2![]() ﹣
﹣![]() π.
π.


科目:初中数学 来源: 题型:
【题目】将二次函数y=x2﹣6x+5用配方法化成y=(x﹣h)2+k的形式,下列结果中正确的是( )
A.y=(x﹣6)2+5
B.y=(x﹣3)2+5
C.y=(x﹣3)2﹣4
D.y=(x+3)2﹣9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的是某中学九(3)班学生外出方式(乘车、步行、骑车)的频数(人数)分布直方图(部分)和扇形分布图,那么下列说法正确的是( )
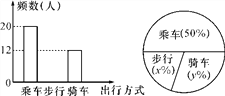
A. 九(3)班外出的学生共有42人
B. 九(3)班外出步行的学生有8人
C. 在扇形图中,步行的学生人数所占的圆心角为82°
D. 如果该校九年级外出的学生共有500人,那么估计全年级外出骑车的学生约有140人
查看答案和解析>>
科目:初中数学 来源: 题型:
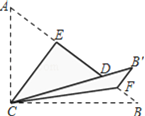
【题目】如图, 在Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:
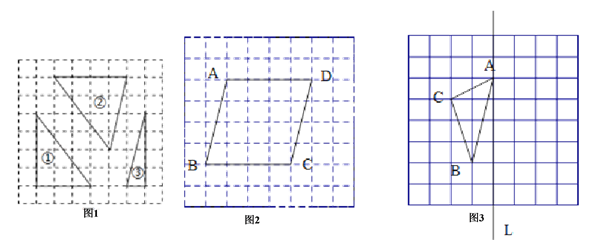
(1)如图,在图1所给方格纸中,每个小正方形边长都是1,标号为①②③的三个三角形均为格点三角形(顶点在方格顶点处),请按要求将图2中的指定图形分割成三个三角形,使它们与标号为①②③的三个三角形分别对应全等.(分割线画成实线.)
(2)如图3,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
①在图中画出与△ABC关于直线L成轴对称的△A′B′C′;
②请直线L上找到一点P,使得PC + PB的距离之和最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com