
 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=1,MC=4,动点P在AB边上,连接PC,PM,则PC+PM的最小值是( )| A. | $\sqrt{17}$ | B. | 6 | C. | $\sqrt{26}$ | D. | 7 |
分析 根据平面内线段最短,构建直角三角形,解直角三角形即可.
解答 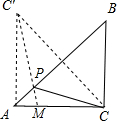 解:如图,过点作CO⊥AB于O,延长BO到C',使OC'=OC,连接MC',交AB于P,
解:如图,过点作CO⊥AB于O,延长BO到C',使OC'=OC,连接MC',交AB于P,
此时PC'=PM+PC'=PM+PC的值最小,
连接AC',
∵CO⊥AB,AC=BC,∠ACB=90°,
∴∠ACO=$\frac{1}{2}$×90°=45°,
∵CO=OC',CO⊥AB,
∴AC'=CA=AM+MC=5,
∴∠OC'A=∠OCA=45°,
∴∠C'AC=90°,
∴C'A⊥AC,
∴MC′=$\sqrt{A{M}^{2}+A{C}^{2}}$=$\sqrt{{1}^{2}+{5}^{2}}$=$\sqrt{26}$,
∴PC+PM的最小值为$\sqrt{26}$.
故选C.
点评 本题考查了线路最短的问题,确定动点P为何位置时,使PC+PM的值最小是关键.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB是半圆O的直径,点C在半圆O上,AB=4cm,∠CAB=60°,P是弧$\widehat{BC}$上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是($\sqrt{13}$-1)cm.
如图,AB是半圆O的直径,点C在半圆O上,AB=4cm,∠CAB=60°,P是弧$\widehat{BC}$上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是($\sqrt{13}$-1)cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1562 | B. | 1806 | C. | 3367 | D. | 3369 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
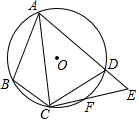 如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为( )
如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
| 每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3,点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE.当点D在边BC上运动时,OE的长度的最小值是5$\sqrt{2}$.
如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3,点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE.当点D在边BC上运动时,OE的长度的最小值是5$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在四边形OABC中,AB∥OC,BC⊥x轴于C,A(1,-1),B(3,-1),动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动.过P作PQ⊥OA于Q.设P点运动的时间为t秒(0<t<2),△OPQ与四边形OABC重叠的面积为S.
在四边形OABC中,AB∥OC,BC⊥x轴于C,A(1,-1),B(3,-1),动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动.过P作PQ⊥OA于Q.设P点运动的时间为t秒(0<t<2),△OPQ与四边形OABC重叠的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在楼顶点A处观察旗杆CD测得旗杆顶部C的仰角为30°,旗杆底部D的俯角为45°.已知楼高AB=9m,则旗杆CD的高度为( )
如图,在楼顶点A处观察旗杆CD测得旗杆顶部C的仰角为30°,旗杆底部D的俯角为45°.已知楼高AB=9m,则旗杆CD的高度为( )| A. | $(9+\sqrt{3})$m | B. | $(9+3\sqrt{3})$m | C. | 9$\sqrt{3}$m | D. | 12$\sqrt{3}$m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com