
分析 先对所求式子化简,然后选取合适的x的值代入即可解答本题,注意x不能取-1,-2.
解答 解:(x-1-$\frac{3}{x+1}$)÷$\frac{{x}^{2}+4x+4}{x+1}$
=$(\frac{{{x^2}-1}}{x+1}-\frac{3}{x+1})×\frac{x+1}{{{{(x+2)}^2}}}$
=$\frac{(x+2)(x-2)}{x+1}×\frac{x+1}{{{{(x+2)}^2}}}$
=$\frac{x-2}{x+2}$
当x=0时,
原式=$\frac{0-2}{0+2}=-1$.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.


科目:初中数学 来源: 题型:填空题
 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为x1=1,x2=-3.
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为x1=1,x2=-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图a和b是相交于点O的两条公路,A,B是两个加油站,现准备在∠AOB的内部建一个油库,要求油库的位置点P既到A,B两个加油站的距离相等,又到两条公路a,b的距离相等,试用尺规作图作出点P.
如图a和b是相交于点O的两条公路,A,B是两个加油站,现准备在∠AOB的内部建一个油库,要求油库的位置点P既到A,B两个加油站的距离相等,又到两条公路a,b的距离相等,试用尺规作图作出点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P是切点,AB=12$\sqrt{3}$,OP=6,则大圆的半径长为( )
如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P是切点,AB=12$\sqrt{3}$,OP=6,则大圆的半径长为( )| A. | 6 | B. | 6$\sqrt{3}$ | C. | 6$\sqrt{2}$ | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
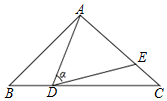 如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,下列结论:
如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点,S△ABC=4平方厘米,则S△BEF的值为( )
如图所示,在△ABC中,已知点D,E,F分别是BC,AD,CE的中点,S△ABC=4平方厘米,则S△BEF的值为( )| A. | 2平方厘米 | B. | 1平方厘米 | C. | $\frac{1}{2}$平方厘米 | D. | $\frac{1}{4}$平方厘米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com