
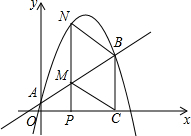 如图,直线y=
如图,直线y=| 1 |
| 2 |
| 17 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
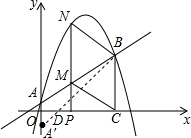
| 5 |
| 2 |
| 17 |
| 4 |
|
|
| 5 |
| 4 |
| 17 |
| 4 |
| 5 |
| 2 |
|
|
| 7 |
| 6 |
| 7 |
| 6 |
| 6 |
| 7 |
| 6 |
| 7 |
| 1 |
| 2 |
| 5 |
| 4 |
| 17 |
| 4 |
| 5 |
| 4 |
| 17 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 15 |
| 4 |
| 5 |
| 4 |
| 15 |
| 4 |
| 5 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
| 5 |
| 4 |
| 3 |
| 2 |
| 45 |
| 16 |
| 3 |
| 2 |
| 45 |
| 16 |
| 5 |
| 4 |
| 15 |
| 4 |
| 5 |
| 2 |
| 5 |
| 4 |
| 15 |
| 4 |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| MP2+PC2 |
(
|
| 5 |
| 2 |
| 5 |
| 4 |
| 15 |
| 4 |
| 5 |
| 2 |
| 1 |
| 2 |
| MP2+PC2 |
| 22+12 |
| 5 |


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
 2013年4月20日早晨8时02分,四川省雅安市芦山县发生7.0级地震,举国上下纷纷捐款捐物.某陶艺班学生积极参与赈灾,决定制作A、B两种型号陶艺品进行义卖,将所得善款全部捐给灾区,制作这两类陶艺品时需用甲、乙两种材料,制作A、B两种型号陶艺品的用料情况如下表所示:
2013年4月20日早晨8时02分,四川省雅安市芦山县发生7.0级地震,举国上下纷纷捐款捐物.某陶艺班学生积极参与赈灾,决定制作A、B两种型号陶艺品进行义卖,将所得善款全部捐给灾区,制作这两类陶艺品时需用甲、乙两种材料,制作A、B两种型号陶艺品的用料情况如下表所示:| 材料 陶艺品 | 甲种材料(kg) | 乙种材料(kg) |
| 1件A型陶艺品 | 0.8 | 0.3 |
| 1件B型陶艺品 | 0.4 | 0.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=
如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=| 2 |
| 3 |
| A、5个 | B、4个 | C、3个 | D、2个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com