
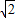 .
.
 ,根据含30°的直角三角形三边的关系得到OD=2OC=2
,根据含30°的直角三角形三边的关系得到OD=2OC=2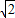 ,CD=
,CD=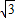 OC=
OC=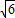 ,则DB=OD-OB=
,则DB=OD-OB=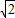 ,利用平行四边形ABDC的周长=2(DB+DC)计算即可;
,利用平行四边形ABDC的周长=2(DB+DC)计算即可; ∠AOB=45°,∠ABO=45°,根据等腰直角三角形的性质得到AB=
∠AOB=45°,∠ABO=45°,根据等腰直角三角形的性质得到AB=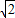 OA=2,而∠CAB=∠BAE,∠ACB=∠ABO,根据相似三角形的判定得到
OA=2,而∠CAB=∠BAE,∠ACB=∠ABO,根据相似三角形的判定得到 AB=
AB= ×2=1,AF=
×2=1,AF=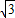 BF=
BF=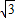 ,
, +1,计算S△ABC:S△AEB=AC2:AB2,=(
+1,计算S△ABC:S△AEB=AC2:AB2,=(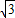 +1)2:22即可.
+1)2:22即可. ,
,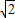
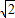 ,CD=
,CD=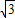 OC=
OC= ,
,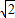 ,
,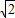 +
+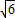 );
); ∠AOB=45°,∠ABO=45°,
∠AOB=45°,∠ABO=45°,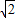 OA=2,
OA=2, AB=
AB= ×2=1,AF=
×2=1,AF=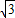 BF=
BF= ,
,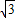 +1,
+1,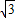 +1)2:22=
+1)2:22= .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (2010•北海)如图,已知⊙O上A、B、C三点,∠BAC=30°,D是OB延长线上的点,∠BDC=30°,⊙O半径为
(2010•北海)如图,已知⊙O上A、B、C三点,∠BAC=30°,D是OB延长线上的点,∠BDC=30°,⊙O半径为| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
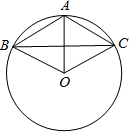 如图,已知⊙O上的三点A、B、C,且AB=AC=6cm,BC=10cm
如图,已知⊙O上的三点A、B、C,且AB=AC=6cm,BC=10cm查看答案和解析>>
科目:初中数学 来源: 题型:
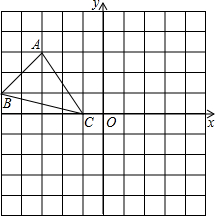 如图,已知网格上最小的正方形的边长为1.
如图,已知网格上最小的正方形的边长为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com